题目内容
甲、乙两名射击运动员,甲射击一次命中10环的概率为0.5,乙射击一次命中10环的概率为s,若他们独立的射击两次,设乙命中10环的次数为X,则EX=
,Y为甲与乙命中10环的差的绝对值.求s的值及Y的分布列及期望.
| 4 |
| 3 |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:先根据X~B(2,S),求出S的值,随机变量Y的取值可以是0,1,2,根据独立试验的概率分别求出P(Y),写出分布列,求出数学期望.
解答:
解:由已知可得X~B(2,S),故EX=2s=
,所以s=
.
随机变量Y的取值可以是0,1,2.
甲、乙两人命中10环的次数都是0次的概率是(
)2×(
)2=
,
甲、乙两人命中10环的次数都是1次的概率是(
×
+
×
)(
×
+
×
)=
,
甲、乙两人命中10环的次数都是2次的概率是(
×
)(
×
)=
所以P(Y=0)=
+
+
=
;
甲命中10环的次数是2且乙命中10环的次数是0次的概率是(
)2×(
)2=
,
甲命中10环的次数是0且乙命中10环的次数是2次的概率是(
×
)(
×
)=
所以P(Y=2)=
+
=
,
故P(Y=1)=1-P(Y=0)-P(Y=2)=
所以Y的分布列是
所以Y的期望是EY=0×
+1×
+2×
=
| 4 |
| 3 |
| 2 |
| 3 |
随机变量Y的取值可以是0,1,2.
甲、乙两人命中10环的次数都是0次的概率是(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 36 |
甲、乙两人命中10环的次数都是1次的概率是(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
甲、乙两人命中10环的次数都是2次的概率是(
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 9 |
所以P(Y=0)=
| 1 |
| 36 |
| 2 |
| 9 |
| 1 |
| 9 |
| 13 |
| 36 |
甲命中10环的次数是2且乙命中10环的次数是0次的概率是(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 36 |
甲命中10环的次数是0且乙命中10环的次数是2次的概率是(
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 9 |
所以P(Y=2)=
| 1 |
| 36 |
| 1 |
| 9 |
| 5 |
| 36 |
故P(Y=1)=1-P(Y=0)-P(Y=2)=
| 1 |
| 2 |
所以Y的分布列是
| Y | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 13 |
| 36 |
| 1 |
| 2 |
| 5 |
| 36 |
| 7 |
| 9 |
点评:本题考查了相互独立事件的概率乘法公式的应用以及随机变量的分布列和数学期望,属于基础题.

练习册系列答案
相关题目
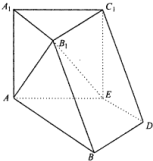 如图,在六面体A1B1C1-ABDE中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AA1⊥AB,四边形AEC1A1是正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1-ABDE中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AA1⊥AB,四边形AEC1A1是正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2. 如图为函数y=Asin(ωx+φ)(A,ω>0,|φ|<π)图象的一段.
如图为函数y=Asin(ωx+φ)(A,ω>0,|φ|<π)图象的一段.