题目内容
13．已知函数y1=（$\frac{1}{2}$）${\;}^{{x}^{2}-3x+1}$与y2=2${\;}^{-{x}^{2}-2x+5}$，若y1＜y2，求实数x的取值范围．分析 把两函数化为同底数，然后由指数函数的单调性化指数不等式为一次不等式求解．
解答 解：∵y1=（$\frac{1}{2}$）${\;}^{{x}^{2}-3x+1}$=${2}^{-{x}^{2}+3x-1}$，y2=2${\;}^{-{x}^{2}-2x+5}$，
且y1＜y2，
∴-x2+3x-1＜-x2-2x+5，
即5x＜6，得x$＜\frac{6}{5}$．
∴实数x的取值范围是（-∞，$\frac{6}{5}$）．
点评 本题考查指数型复合函数的性质及应用，考查了指数不等式的解法，是基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
3．直线l过点M（-1，2），且与以P（-4，-1），Q（3，0）为端点的线段相交，则直线l的斜率的取值范围（ ）
| A． | [-$\frac{1}{2}$，1] | B． | [-2，1] | C． | （-∞，-2]∪[1，+∞） | D． | （-∞，-$\frac{1}{2}$]∪[1，+∞） |
4．函数y=$\frac{1}{x}$在x=$\frac{1}{2}$处的切线与两坐标轴所围成图形的面积是（ ）
| A． | 2 | B． | 3 | C． | $\frac{3}{2}$ | D． | $\frac{5}{2}$ |
8．若函数y=（$\frac{2}{3}$）x，当x∈（0，1）时，其值城为（ ）
| A． | （0，$\frac{2}{3}$） | B． | （$\frac{2}{3}$，1） | C． | （1，+∞） | D． | （0，1） |
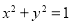上每一点的纵坐标保持不变，横坐标变为原来的2倍得到曲线
．
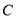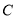的参数方程；
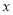轴正半轴为极轴坐标建立极坐标系，已知直线
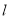的极坐标方程为
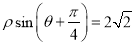，若
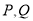分别为曲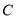线
和直线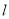
上的一点，求
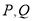的最近距离．
（
是虚数单位）是纯虚数，则实数
（ ）