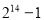题目内容
5.求下列函数的单调区间:(1)f(x)=3x2-2lnx
(2)y=x3+ax(a∈R)
分析 求函数的定义域和导数,利用导数研究函数的单调性,即可得到函数的单调区间.
解答 解:(1)f(x)=3x2-2lnx的定义域为(0,+∞),
则函数的导数f′(x)=6x-$\frac{2}{x}$=$\frac{6{x}^{2}-2}{x}$,
由f′(x)>0得6x2-2>0,即x2>$\frac{1}{3}$,则x>$\frac{\sqrt{3}}{3}$或x<-$\frac{\sqrt{3}}{3}$(舍),即函数的单调递增区间为($\frac{\sqrt{3}}{3}$,+∞),
由f′(x)<0得6x2-2<0,即x2<$\frac{1}{3}$,则-$\frac{\sqrt{3}}{3}$<x<$\frac{\sqrt{3}}{3}$,∵x>0,∴0<x<$\frac{\sqrt{3}}{3}$即函数的单调递减区间为(0,$\frac{\sqrt{3}}{3}$)
(2)y=x3+ax(a∈R)的导数为y′=3x2+a,
若a≥0,则y′≥0恒成立,此时函数单调递增,即函数的单调递增区间为(-∞,+∞),
若a<0,则有由y′>0得x2>-$\frac{a}{3}$,则x>$\sqrt{-\frac{a}{3}}$或x<-$\sqrt{-\frac{a}{3}}$,即函数的单调递增区间为($\sqrt{-\frac{a}{3}}$,+∞),(-∞,-$\sqrt{-\frac{a}{3}}$)
由y′<0得x2<-$\frac{a}{3}$,则-$\sqrt{-\frac{a}{3}}$<x<$\sqrt{-\frac{a}{3}}$,即函数的单调递减区间为(-$\sqrt{-\frac{a}{3}}$,$\sqrt{-\frac{a}{3}}$).
点评 本题主要考查函数单调区间的求解,求函数的导数,利用函数单调性和导数之间的关系是解决本题的关键.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
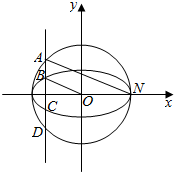 如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的半焦距为c,原点O到经过两点(c、0),(0,b)的直线的距离为λc(λ∈(0,1),垂直于x轴的直线l与椭圆C1及圆C2:x2+y2=a2均有两个交点,这四个交点按其坐标从大到小分别为A、B、C、D
如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的半焦距为c,原点O到经过两点(c、0),(0,b)的直线的距离为λc(λ∈(0,1),垂直于x轴的直线l与椭圆C1及圆C2:x2+y2=a2均有两个交点,这四个交点按其坐标从大到小分别为A、B、C、D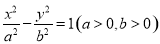 的右焦点
的右焦点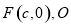 为坐标原点,以
为坐标原点,以 为圆心,
为圆心,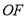 为半径的圆与该双曲线的交点的横坐标为
为半径的圆与该双曲线的交点的横坐标为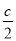 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )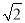 B.
B.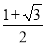 C.2 D.
C.2 D.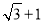
 在点
在点 处的切线与
处的切线与 平行,则
平行,则 ( )
( ) 且
且 ,则实数
,则实数 的取值范围为( )
的取值范围为( ) B.
B.
 D.
D.
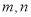 ,定义某种运算“※”,法则如下:当
,定义某种运算“※”,法则如下:当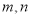 都是正奇数时,
都是正奇数时,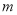 ※
※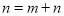 ;当
;当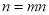 ,则在此定义下,集合
,则在此定义下,集合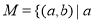 ※
※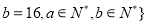 的真子集的个数是( )
的真子集的个数是( )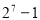 B.
B.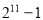 C.
C.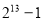 D.
D.