题目内容
4.函数y=$\frac{1}{x}$在x=$\frac{1}{2}$处的切线与两坐标轴所围成图形的面积是( )| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
分析 求得导数,求得切线的斜率和切点,由点斜式方程可得切线的方程,令x=0,y=0可得与坐标轴的交点,再由三角形的面积公式,计算即可得到所求值.
解答 解:函数y=$\frac{1}{x}$的导数为y′=-$\frac{1}{{x}^{2}}$,
即有在x=$\frac{1}{2}$处的切线斜率为-4,
切点为($\frac{1}{2}$,2),
则切线的方程为y-2=-4(x-$\frac{1}{2}$),
令x=0时,可得y=4;
令y=0时,x=1,
则切线与两坐标轴所围成图形的面积是$\frac{1}{2}$×4×1=2.
故选:A.
点评 本题考查导数的运用:求切线的方程,考查直线方程的运用以及三角形的面积的求法,考查运算能力,属于基础题.

练习册系列答案
相关题目
15.点S、A、B、C在半径为$\sqrt{2}$的同一球面上,点S到平面ABC的距离为$\frac{1}{2}$,AB=BC=CA=$\sqrt{3}$,则点S与△ABC中心的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
9.已知sin($\frac{π}{4}$+x)=$\frac{1}{4}$,则cos(x+$\frac{7π}{4}$)等于( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{\sqrt{15}}{4}$ | D. | -$\frac{\sqrt{15}}{4}$ |




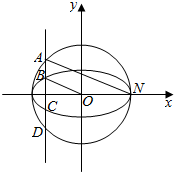 如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的半焦距为c,原点O到经过两点(c、0),(0,b)的直线的距离为λc(λ∈(0,1),垂直于x轴的直线l与椭圆C1及圆C2:x2+y2=a2均有两个交点,这四个交点按其坐标从大到小分别为A、B、C、D
如图,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的半焦距为c,原点O到经过两点(c、0),(0,b)的直线的距离为λc(λ∈(0,1),垂直于x轴的直线l与椭圆C1及圆C2:x2+y2=a2均有两个交点,这四个交点按其坐标从大到小分别为A、B、C、D 且
且 ,则实数
,则实数 的取值范围为( )
的取值范围为( ) B.
B.
 D.
D.