题目内容

设f（x）=ax3+bx3+cx+7（其中a，b，c为常数，x∈R），若f（-7）=-17，则f（7）=（　　）
A、31B、17C、-31D、24
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：假设g（x）=ax3+bx3+cx，有g（x）是个奇函数，f（-7）=g（-7）+7=-17，有g（-7）=-24，g（7）=24故可得f（7）=g（7）+7=24+7=31．
解答： 解：假设g（x）=ax3+bx3+cx，很明显g（x）是个奇函数，
f（-7）=g（-7）+7=-17，g（-7）=-24，
f（7）=g（7）+7=24+7=31    （因为g（7）=24）．
故选：A．
点评：此题主要考查函数奇偶性的性质、求代数式的值，属于中档题．
练习册系列答案
相关题目
计算：
（1）(
1
27
)
1
3
-(6
1
4
)
1
2
+(2
2
)-
2
3
+π0-3-1
（2）已知x+x-1=4（0＜x＜1），求
x2-x-2
x
1
2
+x-
1
2
．
若函数f（x）=x2+（a2-4a+1）x+2在区间（-∞，1]上是减函数，则a的取值范围是
 
．
已知映射f：A→B，A=B=R，对应法则f：x→y=x2-2x-1，对于k∈B，在集合A不存在原象，则k的取值范围是
 
．
若一个圆柱的正视图与其侧面展开图相似，则这个圆柱的侧面积与全面积之比为（　　）
A、
π
π
+1
B、
2
π
2
π
+1
C、
2
2
π
+1
D、
1
π
+1
若全集U={1，2，3，4，5，6}，P={1，2，5}，Q={2，3，4，5}，则∁U（P∪Q）的所有元素的和为
 
．
设函数f（x）=x2-2x+m．
（1）若任意x∈[0，3]，f（x）≥0恒成立，求m的取值范围；
（2）若存在x∈[0，3]，f（x）≥0成立，求m的取值范围．
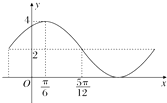已知函数y=Asin（ωx+φ）+b的一部分图象如图所示（A＞0，ω＞0，|φ|＜
π
2
），则函数表达式为（　　）
A、y=2sin（
1
2
x+
5π
12
）+2
B、y=2sin（2x+
π
6
）+2
C、y=4sin（2x+
5π
12
）+2
D、y=4sin（2x+
π
6
）+2
已知集合A={y|y=x2}，B={y|y=-2x2+3}，则A∩B=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网