题目内容

如图所示，则这个几何体的体积等于（　　）
A、4B、6C、8D、12
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：该几何体是四棱锥，底面是直角梯形，一条侧棱垂直底面，根据公式可求体积．
解答： 解：由三视图复原几何体，如图
它的底面是直角梯形，一条侧棱垂直底面高为2，
这个几何体的体积：V=
1
3
×
2+4
2
×2×2=4
故选A．
点评：本题考查三视图、棱锥的体积；考查简单几何体的三视图的运用；考查空间想象能力和基本的运算能力．
练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中，E、F分别是棱AB、BB1的中点，则A1E与CF所成角的余弦值为（　　）
A、
1
2
B、
2
2
C、
21
5
D、
2
5
若一个圆柱的正视图与其侧面展开图相似，则这个圆柱的侧面积与全面积之比为（　　）
A、
π
π
+1
B、
2
π
2
π
+1
C、
2
2
π
+1
D、
1
π
+1
设函数f（x）=x2-2x+m．
（1）若任意x∈[0，3]，f（x）≥0恒成立，求m的取值范围；
（2）若存在x∈[0，3]，f（x）≥0成立，求m的取值范围．
下列选项正确的是（　　）
A、y=cosx的图象向右平移
π
2
得y=sinx的图象
B、y=sinx的图象向右平移
π
2
得y=cosx的图象
C、当φ＜0时，y=sinx向左平移|φ|个单位可得y=sin（x+φ）的图象
D、y=sin（2x+
π
3
）的图象由y=sin2x的图象向左平移
π
3
个单位得到
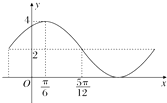已知函数y=Asin（ωx+φ）+b的一部分图象如图所示（A＞0，ω＞0，|φ|＜
π
2
），则函数表达式为（　　）
A、y=2sin（
1
2
x+
5π
12
）+2
B、y=2sin（2x+
π
6
）+2
C、y=4sin（2x+
5π
12
）+2
D、y=4sin（2x+
π
6
）+2
已知：直线l：（2+m）x+（1-2m）y+4-3m=0，不论m为何实数，直线l恒过一定点M，则点M的坐标
 
．
假设关于某设备的使用年限x和所支出的维修费y（万元）有如下的统计资料：
使用年限x23456
维修费用y2.23.85.56.57.0
由资料可知y和x呈线性相关关系，由表中数据算出线性回归方程
∧
y
=
∧
b
x+
∧
a
中的
∧
b
=1.23 据此估计，使用年限为10年时的维修费用是（　　）万元．
A、12.18
B、12.28
C、12.38
D、12.48
在等差数列{an}中，已知a1+a2+a3+a4+a5=20，则a3等于（　　）
A、4B、5C、6D、7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网