题目内容
sin（-
）+2sin
π+3sin
π的值等于 ．
| π |
| 3 |
| 5π |
| 3 |
| 2π |
| 3 |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由条件利用诱导公式进行化简求值．
解答：
解：sin（-
）+2sin
π+3sin
π=-sin
+2sin（2π-
）+3sin（π-
）
=-sin
-2sin
+3sin
=0，
故答案为：0．
| π |
| 3 |
| 5π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=-sin
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故答案为：0．
点评：本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
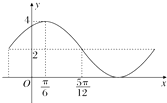已知函数y=Asin（ωx+φ）+b的一部分图象如图所示（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、y=2sin（
| ||||
B、y=2sin（2x+
| ||||
C、y=4sin（2x+
| ||||
D、y=4sin（2x+
|
在等差数列{an}中，已知a1+a2+a3+a4+a5=20，则a3等于（ ）
| A、4 | B、5 | C、6 | D、7 |
已知集合M={x||x|≥x2}，N={x|y=2x-1，x∈R}，则M∩N=（ ）
| A、（0，1] |
| B、（0，1） |
| C、[0，1） |
| D、[0，1] |