题目内容
定积分
0sintcostdt= ．
| ∫ |
0 |
考点：定积分
专题：导数的概念及应用
分析：根据积分公式进行求解即可．
解答：
解：
0sintcostdt=
0sin2td（2t）=
（-cos2t）|
=
×（1+1）=
．
故答案为：
| ∫ |
0 |
| 1 |
| 2 |
| ∫ |
0 |
| 1 |
| 4 |
0 |
| 1 |
| 4 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题主要考查积分的计算，比较基础．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
在R上定义运算?：x?y=x（1-y）若对任意x＞2，不等式（x-a）?x≤a-2都成立，则实数a的取值范围是（ ）
| A、（-∞，3） |
| B、（-∞，3] |
| C、（3，+∞） |
| D、[3，+∞） |
设函数f（x）是定义在（-∞，0）上的可导函数，起到函数为f′（x），且有xf′（x）＞x2+2f（x），则不等式4f（x+2015）-（x+2015）2f（-2）＞0的解集为（ ）
| A、（-∞，2017） |
| B、（-2017，0） |
| C、（-∞，-2016） |
| D、（-2016，0） |
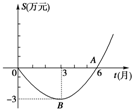2009年某个体企业受金融危机和国家政策调整的影响，经历了从亏损到盈利的过程，下面的二次函数图象（部分）刻画了该公司年初以来的累积利润S（万元）与时间t（月）之间的关系（即前t个月的利润总和S与t之间的关系，0≤t≤12）．请根据图象提供的信息解答下列问题：