题目内容
2.已知函数 f(x)=1+x-$\frac{x^2}{2}$+$\frac{x^3}{3}$,g (x)=1-x+$\frac{{x}^{2}}{2}$-$\frac{x^3}{3}$,设函数F(x)=f(x-4)?g(x+3),且函数 F ( x) 的零点均在区间[a,b]( a<b,a,b∈Z )内,则 b-a 的最小值为6.分析 求出函数f(x)的导数,求出f(x)的单调区间,从而求出其零点的范围,求出f(x-4)的零点所在的范围;通过讨论x的范围,求出g(x)在R的导数,得到g(x)的单调区间,从而求出g(x+3)所在的零点的范围,F ( x) 的零点均在区间[a,b],进而求出a,b的值,求出答案即可.
解答 解:∵函数 f(x)=1+x-$\frac{x^2}{2}$+$\frac{x^3}{3}$,f′(x)=1-x+x2>0,∴f(x)在R单调递增,而f(0)=1>0,f(-1)=1-1-$\frac{1}{2}$+$\frac{1}{3}$<0,
∴函数f(x)在区间(-1,0)内有零点,∴函数f(x-4)在[3,4]上有一个零点,
函数g (x)=1-x+$\frac{{x}^{2}}{2}$-$\frac{x^3}{3}$,g′(x)=-1+x-x2<0,∴f(x)在R单调递减,而g(1)=1-1+$\frac{1}{2}$$-\frac{1}{3}$>0,g(2)=1-2+2$-\frac{8}{3}$<0,
∴函数g(x)在区间(1,2)内有零点,∴函数g(x+3)在[-2,-1]上有一个零点,
函数F(x)=f(x-4)?g(x+3),且函数 F ( x) 的零点在区间[-2,4]内,
则 b-a 的最小值为:6.
故答案为:6.
点评 本题考查函数的单调性的应用,函数的零点的求法,考查转化思想以及计算能力.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
13.命题p:若a>b,则ac2>bc2;命题q:?x0>0,使得x0-1+lnx0=0,则下列命题为真命题的是( )
| A. | p∧q | B. | (¬p)∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
10.已知集合A={x||x+1|≥1},B={x|x≥-1},则(∁RA)∩B=( )
| A. | [-1,0] | B. | [-1,0) | C. | (-2,-1) | D. | (-2,-1] |
17.已知 x>1,y>1,且 lg x,$\frac{1}{4}$,lg y 成等比数列,则 xy 有( )
| A. | 最小值10 | B. | 最小值$\sqrt{10}$ | C. | 最大值10 | D. | 最大值 $\sqrt{10}$ |
7.已知 x>1,y>1,且 lg x,2,lg y 成等差数列,则 x+y 有( )
| A. | 最小值 20 | B. | 最小值 200 | C. | 最大值 20 | D. | 最大值 200 |
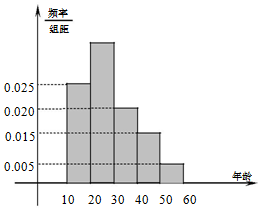 •滑雪场开业当天共有 500 人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取 20 人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.
•滑雪场开业当天共有 500 人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取 20 人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.