题目内容
4.已知命题p:?x∈R,cosx>sinx,命题q:?x∈(0,π),sinx+$\frac{1}{sinx}$>2,则下列判断正确的是( )| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
分析 命题p:取x=0∈R,cosx>sinx成立,即可判断出真假.命题q:取x=$\frac{π}{2}$时,$sin\frac{π}{2}$+$\frac{1}{sin\frac{π}{2}}$=2,此时不成立,即可判断出真假,再利用复合命题真假的判定方法即可得出.
解答 解:命题p:?x=0∈R,cosx>sinx,因此是真命题.
命题q:?x∈(0,π),sinx+$\frac{1}{sinx}$>2,是假命题,取x=$\frac{π}{2}$时,$sin\frac{π}{2}$+$\frac{1}{sin\frac{π}{2}}$=2,此时不成立,因此是假命题.
则下列判断正确的是:命题p∧(¬q)是真命题.
故选:D.
点评 本题考查了三角函数的单调性及其值域、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
14.某次军事演习要出动一艘航母,2艘攻击型潜艇一前一后,3艘驱逐舰和3艘护卫舰分列左右,每侧3艘,同侧不能都是同种舰艇,则舰艇分配方案的方法数为( )
| A. | 72 | B. | 324 | C. | 648 | D. | 1296 |
19.某班级要从4名男生、2名女生中选派4人参加某次社区服务,则所选的4人中至少有1名女生的概率为( )
| A. | $\frac{14}{15}$ | B. | $\frac{8}{15}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{15}$ |
16.命题“?x∈R,sinx>1”的否定是( )
| A. | ?x∈R,sinx≤1 | B. | ?x∈R,sinx>1 | C. | ?x∈R,sinx=1 | D. | ?x∈R,sinx≤1 |
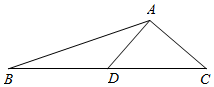 已知如图,△ABC中,AD是BC边的中线,∠BAC=120°,且$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{15}{2}$.
已知如图,△ABC中,AD是BC边的中线,∠BAC=120°,且$\overrightarrow{AB}•\overrightarrow{AC}$=-$\frac{15}{2}$.