题目内容
15.在△ABC中,角A,B,C所对的边分别为a,b,c,且3acosA=bcosC+ccosB(1)求cosA
(2)若a=3,求△ABC的面积的最大值.
分析 (1)根据正弦定理将边化角,利用两角和的正弦函数公式化简得出cosA;
(2)利用余弦定理和基本不等式得出bc的最大值,代入三角形的面积公式求出面积最大值.
解答 解:(1)在△ABC中,∵3acosA=bcosC+ccosB,
∴3sinAcosA=sinBcosC+sinCcosB=sin(B+C)=sinA,即3sinAcosA=sinA,
又A∈(0,π),∴sinA≠0,
∴$cosA=\frac{1}{3}$.
(2)∵a2=b2+c2-2bccosA,即${b^2}+{c^2}-\frac{2}{3}bc=9$,∴b2+c2=9+$\frac{2}{3}$bc≥2bc,∴$bc≤\frac{27}{4}$.
∵sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{2\sqrt{2}}{3}$,
∴△ABC的面积$S=\frac{1}{2}bcsinA$$≤\frac{1}{2}•\frac{27}{4}•\frac{{2\sqrt{2}}}{3}=\frac{{9\sqrt{2}}}{4}$,($b=c=\frac{{3\sqrt{3}}}{2}$时取等号)
∴${S_{max}}=\frac{{9\sqrt{2}}}{4}$.
点评 本题考查了正弦定理,余弦定理,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
3.等差数列{an}的首项a1=-5,它的前11项的平均值为5,若从中抽去一项,余下的10项的平均值为4.6,则抽去的是( )
| A. | a6 | B. | a8 | C. | a9 | D. | a10 |
10.把复数z的共轭复数记作$\overline z$,已知(3-4i)$\overline z$=1+2i,则z=( )
| A. | $\frac{1}{5}$+$\frac{2}{5}$i | B. | -$\frac{1}{5}$+$\frac{2}{5}$i | C. | -$\frac{1}{5}$-$\frac{2}{5}$i | D. | $\frac{1}{5}$-$\frac{2}{5}i$ |
20.若不等式组$\left\{{\begin{array}{l}{x+3y-4≥0}\\{3x+y-4≤0}\\{x≥0}\end{array}}\right.$所表示的平面区域被直线y=kx+$\frac{4}{3}$分为面积相等的两部分,则k的值是( )
| A. | $\frac{3}{7}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
7.已知函数f(x)=(x-a-1)(2x-a),g(x)=ln(x-a),若当x>a时,f(x)•g(x)≥0恒成立,则实数a的取值范围是( )
| A. | [0,+∞) | B. | [-2,0] | C. | (-∞,2] | D. | [-2,+∞) |
4.已知命题p:?x∈R,cosx>sinx,命题q:?x∈(0,π),sinx+$\frac{1}{sinx}$>2,则下列判断正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
5.直线x-2y+1=0与直线2x+ay-3=0相互垂直,则实数a的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
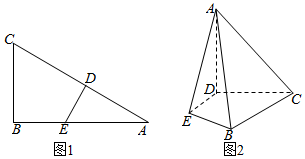 已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).
已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).