题目内容
8.下列关系式中,根式与分数指数幂互化正确的是( )| A. | $\root{3}{a}$•$\sqrt{-a}$=-a${\;}^{\frac{5}{6}}$ | B. | x${\;}^{\frac{2}{4}}$=$\sqrt{x}$ | C. | ($\root{3}{{b}^{\frac{3}{2}}}$)${\;}^{\frac{3}{2}}$=b3 | D. | (a-b)${\;}^{-\frac{5}{2}}$=$\sqrt{(a-b)^{-5}}$ |
分析 根据各式是否有意义,是否符合根式与分数指数幂的互相转化规律进行判断.
解答 解:对于A,由$\sqrt{-a}$有意义可知a≤0,而当a<0时,a${\;}^{\frac{5}{6}}$=$\root{6}{{a}^{5}}$无意义,故A错误;
对于B,当x<0时,x${\;}^{\frac{2}{4}}$=$\root{4}{{x}^{2}}$,而$\sqrt{x}$无意义,故B错误;
对于C,($\root{3}{{b}^{\frac{3}{2}}}$)${\;}^{\frac{3}{2}}$=(b${\;}^{\frac{1}{2}}$)${\;}^{\frac{3}{2}}$=b${\;}^{\frac{3}{4}}$,故C错误.
对于D,(a-b)${\;}^{-\frac{5}{2}}$=$\frac{1}{\sqrt{(a-b)^{5}}}$=$\sqrt{\frac{1}{(a-b)^{5}}}$=$\sqrt{(a-b)^{-5}}$.故D正确.
故选D.
点评 本题考查了分数指数幂与根式的互相转化,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.若f(x)=x+$\frac{4}{x}$,则下列结论正确的是( )
| A. | f(x)的最小值为4 | |
| B. | f(x)在(0,2)上单调递减,在(2,+∞)上单调递增 | |
| C. | f(x)的最大值为4 | |
| D. | f(x)在(0,2)上单调递增,在(2,+∞)上单调递减 |
12.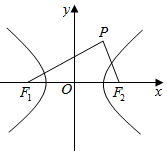 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )| A. | y=±$\frac{1}{2}$x | B. | y=±$\frac{\sqrt{5}}{5}$x | C. | y=±$\frac{2\sqrt{5}}{5}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
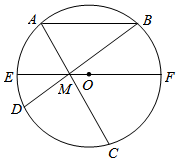 如图,EF是圆O的直径,AB∥EF,点M在EF上,AM、BM分别交圆O于点C、D.设圆O的半径是r,OM=m.
如图,EF是圆O的直径,AB∥EF,点M在EF上,AM、BM分别交圆O于点C、D.设圆O的半径是r,OM=m.