题目内容
12.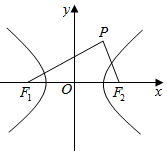 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在第一象限,且满足($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,|$\overrightarrow{{F}_{2}P}$|=a,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )| A. | y=±$\frac{1}{2}$x | B. | y=±$\frac{\sqrt{5}}{5}$x | C. | y=±$\frac{2\sqrt{5}}{5}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
分析 连接F1Q,由向量共线定理可得|F2Q|=$\frac{a}{5}$,|PQ|=$\frac{4a}{5}$,由双曲线的定义可得|F1Q|=$\frac{11a}{5}$,运用向量的数量积的性质可得|F1F2|=|F1P|=2c,在△F1PQ和△QF1F2中,由∠PQF1+∠F2QF1=π,可得cos∠PQF1+cos∠F2QF1=0,运用余弦定理,化简整理可得b=$\frac{1}{2}$a,运用双曲线的渐近线方程即可得到.
解答  解:连接F1Q,由|$\overrightarrow{{F}_{2}P}$|=a,$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,
解:连接F1Q,由|$\overrightarrow{{F}_{2}P}$|=a,$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,
可得|F2Q|=$\frac{a}{5}$,|PQ|=$\frac{4a}{5}$,
由双曲线的定义可得|F1Q|-|F2Q|=2a,
即有|F1Q|=$\frac{11a}{5}$,
由($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,
即为($\overrightarrow{{F}_{1}P}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•($\overrightarrow{{F}_{1}P}$-$\overrightarrow{{F}_{1}{F}_{2}}$)=0,
即有$\overrightarrow{{F}_{1}P}$2-$\overrightarrow{{F}_{1}{F}_{2}}$2=0,|F1F2|=|F1P|=2c,
在△F1PQ和△QF1F2中,由∠PQF1+∠F2QF1=π,可得cos∠PQF1+cos∠F2QF1=0,
由余弦定理可得,$\frac{(\frac{11a}{5})^{2}+(\frac{4a}{5})^{2}-4{c}^{2}}{2•\frac{11a}{5}•\frac{4a}{5}}$+$\frac{(\frac{a}{5})^{2}+(\frac{11a}{5})^{2}-4{c}^{2}}{2•\frac{a}{5}•\frac{11a}{5}}$=0,化简可得c2=$\frac{5}{4}$a2,
由c2=a2+b2,可得b=$\frac{1}{2}$a,可得双曲线的渐近线方程为y=±$\frac{b}{a}$x,即为y=±$\frac{1}{2}$x.
故选:A.
点评 本题考查双曲线的渐近线方程的求法,注意运用三角形中的余弦定理,同时考查向量数量积的性质和向量共线定理的运用,考查化简整理的运算能力,属于中档题.

| A. | $\root{3}{a}$•$\sqrt{-a}$=-a${\;}^{\frac{5}{6}}$ | B. | x${\;}^{\frac{2}{4}}$=$\sqrt{x}$ | C. | ($\root{3}{{b}^{\frac{3}{2}}}$)${\;}^{\frac{3}{2}}$=b3 | D. | (a-b)${\;}^{-\frac{5}{2}}$=$\sqrt{(a-b)^{-5}}$ |
| A. | (0,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,1) | C. | (1,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,+∞) |