题目内容
已知函数f(x)=-
sin2x+sinxcosx,求f(
).
| 3 |
| π |
| 6 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:法1:利用三角函数的倍角公式,将函数进行化简,即可进行求值.
法2:因为
是特殊角,可以直接代入进行求解.
法2:因为
| π |
| 6 |
解答:
解:法1:∵f(x)=-
sin2x+sinxcosx=-
×
+
sin2x=
cos2x+
sin2x-
,
∴f(
)=
cos(2×
)+
sin(2×
)-
=
×
+
×
-
=
-
=0,
法2:∵f(x)=-
sin2x+sinxcosx,
∴f(
)═-
sin2
+sin
cos
=-
×
+
×
=0.
| 3 |
| 3 |
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴f(
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
法2:∵f(x)=-
| 3 |
∴f(
| π |
| 6 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题主要考查三角函数值的计算,比较基础.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
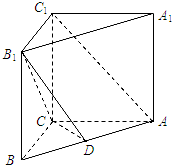 如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.