题目内容
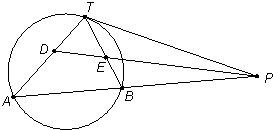如图，PT是⊙O的切线，切点为T，直线PA与⊙O交于A、B两点，∠TPA的平分线分别交直线TA、TB于D、E两点，已知PT=2，PB=| 3 |
| TE |
| AD |
分析：由图形知，线段PA的长度可以用切割线定理建立方程来求，由PT2=PB×PA即可求解；观察发现TE与AD分别在两个三角形PTE与三角形PDA中，而此两个三角形可以证出是相似的，由此可求得
．
| TE |
| AD |
解答：解：由题意，如图可得PT2=PB×PA
又由已知PT=2，PB=
，故可得PA=
又TPA的平分线分别交直线TA、TB于D、E两点，可得
∠TPE=∠APD
又由弦切角定理知∠PTE=∠PAD
故有△PET≈△PDA
故有TE：AD=PT：PA=
：2
故答案为
，
又由已知PT=2，PB=
| 3 |
| 4 |
| 3 |
| 3 |
又TPA的平分线分别交直线TA、TB于D、E两点，可得
∠TPE=∠APD
又由弦切角定理知∠PTE=∠PAD
故有△PET≈△PDA
故有TE：AD=PT：PA=
| 3 |
故答案为
| 4 |
| 3 |
| 3 |
| ||
| 2 |
点评：本题考点是与圆有关的比例线段，考查圆中的相关定理与性质，本题中考查到了用切割线定理建立方程求线段的长度，以及利用三角形的相似求两个线段的比值．本题做题时要注意分析图形的结构，切实从图形中观察出等式建立的依据，或者相关线之间的位置关系，以方便利用这些条件组合出解题的思路、方法．
练习册系列答案
相关题目
（2012•徐州模拟）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，
（2012•江苏三模）选修4-1：几何证明选讲如图，P是半圆O的直径BC延长线上一点，PT切半圆于点T，TH⊥BC于H，若PT=1，PB+PC=2a，则PH=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
