Question

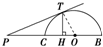
如图，P是半圆O的直径BC延长线上一点，PT切半圆于点T，TH⊥BC于H，若PT=1，PB+PC=2a，则PH=（　　）

• A、

  2

  a

• B、

  1

  a

• C、

  a

  2

• D、

  a

  3

Answer 1

分析：连接OT，由PT=1、PB+PC=2a，利用切割线定理算出BC长．再根据题意证出△TPH∽△OPT，通过三角形的相似比可算出PH的长．

解答：解：如图，连接OT．
∵PT²=PC•PB，PT=1且PB+PC=2a
∴BC=PB-PC=

(PB+PC)2-4PB•PC

=2

a2-1

∴OT=OC=

a2-1

，可得OP=

PT2+OT2

=a．
又∵∠TPH=∠OPT，∠PTO=∠PHT=90°
∴△TPH∽△OPT，可得

PH

PT

=

PT

PO

，PH=

PT2

PO

=

1

a

．
故选：B

点评：本题给出半圆满足的条件，求线段PH长．着重考查了切割线定理、相似三角形的判定与性质等知识，属于中档题．