题目内容
4.椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,其左焦点到点P(2,1)的距离为$\sqrt{10}$.(Ⅰ)求椭圆的标准方程;
(Ⅱ)是否存在过(0,-2)的直线l与椭圆C相交于A,B两点,且以AB为直径的圆过椭圆C的右顶点,若存在,求出直线l的方程,不存在请说明理由.
分析 (Ⅰ)由题意可知:椭圆的由离心率e=$\frac{c}{a}$=$\frac{1}{2}$,即a=2c,左焦点F(-c,0)到点P(2,1)的距离为$\sqrt{10}$,即(2+c)2+1=10,解得:c=1,由b2=a2-c2=3,即可求得椭圆方程;
(Ⅱ)当直线斜率存在,设直线l的方程y=kx-2,代入椭圆方程,△>0,解得k2>$\frac{1}{4}$,y1•y2=(kx1-2)(kx2-2)=$\frac{12-12{k}^{2}}{4{k}^{2}+3}$,以AB为直径的圆过椭圆C的右顶点M(2,0),$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,整理得:k2-8k+7=0,即可求得k=7或k=1,满足k2>$\frac{1}{4}$,即可求得直线l的方程.
解答 解:(Ⅰ)由椭圆的由离心率e=$\frac{c}{a}$=$\frac{1}{2}$,即a=2c,
左焦点F(-c,0)到点P(2,1)的距离为$\sqrt{10}$,即(2+c)2+1=10,解得:c=1,
则a=2,由b2=a2-c2=3,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,;
(Ⅱ)设满足条件的直线存在,①当直线的斜率不存在是,显然不符合题意,
②当直线斜率存在,设直线l的方程y=kx-2,直线l和圆C的交点为A (x1,y1),B(x2,y2)
∴$\left\{\begin{array}{l}{y=kx-2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:(4k2+3)x2-16kx+4=0,
由△=256k2-16(4k2+3)>0,解得:k2>$\frac{1}{4}$,
由韦达定理可知:x1+x2=$\frac{16k}{4{k}^{2}+3}$,x1•x2=$\frac{4}{4{k}^{2}+3}$,
y1•y2=(kx1-2)(kx2-2)=k2x1•x2-2k(x1+x2)+4=k2×$\frac{4}{4{k}^{2}+3}$-2k×$\frac{16k}{4{k}^{2}+3}$+4=$\frac{12-12{k}^{2}}{4{k}^{2}+3}$,
以AB为直径的圆过椭圆C的右顶点M(2,0),
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,
由$\overrightarrow{MA}$=(x1-2,y1),$\overrightarrow{MB}$=(x2-2,y2),
∴(x1-2)(x2-2)+y1•y2=0,
∴$\frac{4}{4{k}^{2}+3}$-2×$\frac{16k}{4{k}^{2}+3}$+4+$\frac{12-12{k}^{2}}{4{k}^{2}+3}$=0,
整理得:k2-8k+7=0,解得:k=7或k=1,满足k2>$\frac{1}{4}$,
∴y=x-2或y=7x-2,
出直线l的方程y=x-2或y=7x-2.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查向量数量积的坐标表示,韦达定理的应用,考查计算能力,属于中档题.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案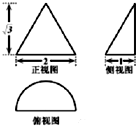
| A. | $\frac{\sqrt{3}π}{2}$ | B. | $\frac{\sqrt{3}π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{\sqrt{3}π}{6}$ |
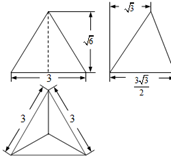
| A. | $\frac{{9\sqrt{3}}}{4}$ | B. | $9\sqrt{3}$ | C. | $\frac{{9\sqrt{2}}}{4}$ | D. | $9\sqrt{6}$ |
| A. | $\frac{1}{4032π}$ | B. | $\frac{1}{2016π}$ | C. | $\frac{1}{4032}$ | D. | $\frac{1}{2016}$ |
 中,如果
中,如果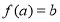 ,那么称
,那么称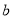 为
为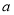 的像.设
的像.设 ,
,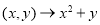 ,则
,则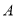 中所有元素的像构成的集合是______.(用列举法表示)
中所有元素的像构成的集合是______.(用列举法表示)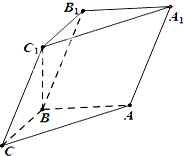 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.