题目内容
17.若下列方程:x2+4ax-4a+3=0,x2+2ax-2a=0,x2+(a-1)x+a2=0至少有一个方程有实根,则实数a的取值范围为{a|a≥-1或a≤-$\frac{3}{2}$}..分析 假设三个方程均没有实数根,即三个判别式均小于0,得到-$\frac{3}{2}$<a<-1,再取其对应集合的补集即可.
解答 解:假设没有一个方程有实数根,则:
16a2-4(3-4a)<0(1),
(a-1)2-4a2<0(2),
4a2+8a<0(3)(5分),
解之得:-$\frac{3}{2}$<a<-1(10分),
故三个方程至少有一个方程有实根的a的取值范围是:{a|a≥-1或a≤-$\frac{3}{2}$}.(12分)
点评 本题考查二次函数的性质,突出考查判别式法的应用,考查逆向思维,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则 的取值范围是_________.
的取值范围是_________. 中,如果
中,如果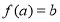 ,那么称
,那么称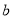 为
为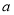 的像.设
的像.设 ,
,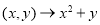 ,则
,则 中所有元素的像构成的集合是______.(用列举法表示)
中所有元素的像构成的集合是______.(用列举法表示)