题目内容
4.求数列{(2n-1)•3n}前n项和.分析 直接利用错位相减法求得答案.
解答 解:由an=(2n-1)3n,得
数列的前n项和Sn=1•3+3•32+…+(2n-1)•3n,
∴3Sn=1•32+3•33+…+(2n-3)•3n+(2n-1)•3n+1,
两式作差得:-2Sn=1•3+2(32+33+…+3n)-(2n-1)•3n+1
=3+2×$\frac{9(1-{3}^{n-1})}{1-3}$-(2n-1)•3n+1=-2(n-1)•3n+1-6.
∴Sn=(n-1)•3n+1+3.
点评 本题考查数列的求和,训练了错位相减法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的定义域为
的定义域为 ,值域为
,值域为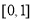 ,那么满足条件的整数对
,那么满足条件的整数对 共有( )
共有( ) 的定义域是
的定义域是 ,则函数
,则函数 的定义域是( )
的定义域是( ) B.
B.
 D.
D.