题目内容
关于x的不等式x2-ax+1≤0的解集中整数只有1,则a的取值范围是( )
A、2≤a<
| ||
B、2<a≤
| ||
C、2≤a≤
| ||
D、2<a<
|
考点:一元二次不等式的解法
专题:函数的性质及应用
分析:根据函数f(x)=x2-ax+1的图象与性质,列出不等式组,求出解集即可.
解答:
解:∵不等式x2-ax+1≤0的解集中整数只有1,
∴设f(x)=x2-ax+1,
则
,
即
;
解得2≤a<
;
∴a的取值范围是2≤a<
.
故选:A.
∴设f(x)=x2-ax+1,
则
|
即
|
解得2≤a<
| 5 |
| 2 |
∴a的取值范围是2≤a<
| 5 |
| 2 |
故选:A.
点评:本题考查了二次函数的图象与性质的应用问题,也考查了不等式的解法与应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的左右焦点分别为F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
已知双曲线
-
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于M,N两点,O为坐标原点,若双曲线的离心率为2,△MON的面积为
,则P的值为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
| B、3 | ||
| C、4 | ||
| D、2 |
若x∈R,则“x<1”是“|x|<1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
双曲线x2-2y2=1的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
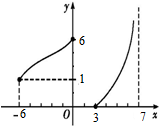 函数y=f(x)的图象如图所示,则函数y=f(x)的定义域为
函数y=f(x)的图象如图所示,则函数y=f(x)的定义域为