题目内容
已知面积为S的凸四边形中,四条边长分别记为a1,a2,a3,a4,点P为四边形内任意一点,且点P到四边的距离分别记为h1,h2,h3,h4,若
=
=
=
=k,则h1+2h2+3h3+4h4=
类比以上性质,体积为y的三棱锥的每个面的面积分别记为Sl,S2,S3,S4,此三棱锥内任一点Q到每个面的距离分别为H1,H2,H3,H4,若
=
=
=
=K,则H1+2H2+3H3+4H4=( )
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
| 2S |
| k |
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S4 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:类比推理
专题:计算题,推理和证明
分析:由
=
=
=
=k可得ai=ik,P是该四边形内任意一点,将P与四边形的四个定点连接,得四个小三角形,四个小三角形面积之和为四边形面积,即采用分割法求面积;同理对三棱值得体积可分割为5个已知底面积和高的小棱锥求体积.
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
解答:
解:根据三棱锥的体积公式V=
Sh,
得:
S1H1+
S2H2+
S3H3+
S4H4=V
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+2H2+3H3+4H4=
,
故选B.
| 1 |
| 3 |
得:
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+2H2+3H3+4H4=
| 3V |
| K |
故选B.
点评:本题主要考查三棱锥的体积计算和运用类比思想进行推理的能力.解题的关键是理解类比推理的意义,掌握类比推理的方法.平面几何的许多结论,可以通过类比的方法,得到立体几何中相应的结论.当然,类比得到的结论是否正确,则是需要通过证明才能加以肯定的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的左右焦点分别为F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
若x∈R,则“x<1”是“|x|<1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
双曲线x2-2y2=1的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
已知tanθ=2,则2sin2θ+sinθcosθ-cos2θ=( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
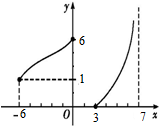 函数y=f(x)的图象如图所示,则函数y=f(x)的定义域为
函数y=f(x)的图象如图所示,则函数y=f(x)的定义域为