题目内容
设数列{an} 的前n项和为Sn,满足2Sn=an+1﹣2n+1+1,n∈N*,且a1,a2+5,a3成等差数列.
(1)求a1,a2,a3的值;
(2)求证:数列{an+2n}是等比数列
(3)证明:对一切正整数n,有 +
+ +…+
+…+ <
< .
.

练习册系列答案
相关题目
已知函数f(x)在R上满足f(x)=2f(2﹣x)﹣x2+8x﹣8,则曲线y=f(x)在点 (1,f(1))处切线的斜率是 ( )
|
| A. | 2 | B. | 1 | C. | 3 | D. | ﹣2 |
 ,得
,得 ,
, ,所以
,所以 .
. ,所以
,所以 是首项为3,公比为3的等比数列.
是首项为3,公比为3的等比数列. ,所以
,所以 ,
, ,两边同时相乘得
,两边同时相乘得 ,
, .
.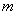 ),则这个几何体的体积为__________
),则这个几何体的体积为__________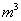
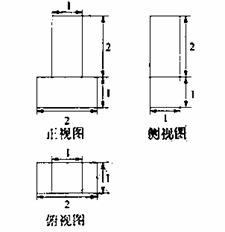

 ,且
,且 ,
, ,求
,求 和
和 .
. 关于原点
关于原点 对称的圆的方程为( )
对称的圆的方程为( ) B.
B.
 D.
D.
 ”是“
”是“ ”的充分不必要条件,则实数
”的充分不必要条件,则实数 的取值范围是___________
的取值范围是___________  为
为 上的可导函数,当
上的可导函数,当 时,
时, ,则关于的函数
,则关于的函数 的零点个数为( )
的零点个数为( ) (
( 为坐标原点),点
为坐标原点),点 ,现向圆
,现向圆 ,则点
,则点 到直线
到直线 的距离小于
的距离小于 的概率为( )
的概率为( ) B、
B、 D、
D、