题目内容
4.已知f(x)=-x2+ax+3.(1)当a=2时,求f(x)的单调递增区间;
(2)若f(x)为偶函数,求f(x)在[-1,3]的最大值与最小值.
分析 (1)求出函数f(x)的对称轴,根据二次函数的性质求出函数的单调区间即可;(2)求出f(x)的解析式,根据二次函数的性质求出函数在[-1,3]的最值即可.
解答 解:(1)当a=2时,f(x)=-x2+2x+3=-(x-1)2+4,
函数的对称轴是:x=1,开口向下,
故f(x)的单调递增区间为(-∞,1].
(2)f(x)为偶函数,则f(-x)=f(x),解得a=0,
则f(x)=-x2+3,f(x)在[-1,0)递增,在(0,3]递减,
故x=0时f(x)有最大值3,x=3时f(x)有最小值-6.
点评 本题考查了二次函数的性质,考查函数的单调性和最值问题,是一道基础题.

练习册系列答案
相关题目
9.设实数x,y满足约束条件$\left\{\begin{array}{l}2x-y-1≥0\\ x-2y+1≤0\\ x+y-5≤0\end{array}\right.$,则当z=ax+by(a>0,b>0)取得最小值2时,a=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
16.下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:
(1)求用最小二乘法得到的回归直线方程(参考公式和数据:$\widehat{y}$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\sum_{i=1}^{5}$xiyi=4010);
(2)请估计该市一面积为120m2的新电梯房的房价.
| x | 7 | 9 | 10 | 11 | 13 |
| y | 40 | 75 | 70 | 90 | 105 |
(2)请估计该市一面积为120m2的新电梯房的房价.
14.设i为虚数单位,复数z满足$\frac{(1+i)^{2}}{z}$=1-i,则复数$\overline{z}$=( )
| A. | -1-i | B. | 1-i | C. | -1+i | D. | 1+i |
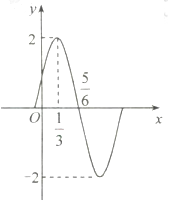 已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.
已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.