题目内容
8.已知定义在R上的函数f(x)满足f(x)=-f(x+$\frac{3}{2}$),且f(-2)=f(-1)=-1,f(0)=2,则f(1)+f(2)+f(3)+…+f(2015)=-2.分析 根据f(x)=-f(x+$\frac{3}{2}$),可以确定函数f(x)的周期为3,利用条件求出函数一个周期内的函数值的和,即可求得f(1)+f(2)+…+f(2015)的值.
解答 解:∵f(x)=-f(x+$\frac{3}{2}$),即f(x+$\frac{3}{2}$)=-f(x),
∴f(x+3)=-f(x+$\frac{3}{2}$)=f(x),
故函数f(x)为周期函数,且周期为3,
∵f(0)=2,f(-2)=f(-1)=-1
f(1)=f(-2+3)=f(-2)=-1,f(2)=f(-3+2)=f(-1)=-1,
∴f(1)+f(2)+f(3)=0,
∴f(1)+f(2)+…+f(2015)=671×[f(1)+f(2)+f(3)]+f(1)+f(2)=671×0-1-1=-2,
故答案为:-2.
点评 本题考查了函数的周期性的应用.解题的关键是寻找到函数f(x)的周期为3,利用周期性将所求表达式转化为简单数值的求解.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.检验双向分类列联表数据下,两个分类特征(即两个因素变量)之间是彼此相关还是相互独立的问题,在常用的方法中,最为精确的做法是( )
| A. | 三维柱形图 | B. | 二维条形图 | C. | 等高条形图 | D. | 独立性检验 |
16.下表是随机抽取的某市五个地段五种不同户型新电梯房面积x(单位:十平方米)和相应的房价y(单位:万元)统计表:
(1)求用最小二乘法得到的回归直线方程(参考公式和数据:$\widehat{y}$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\sum_{i=1}^{5}$xiyi=4010);
(2)请估计该市一面积为120m2的新电梯房的房价.
| x | 7 | 9 | 10 | 11 | 13 |
| y | 40 | 75 | 70 | 90 | 105 |
(2)请估计该市一面积为120m2的新电梯房的房价.
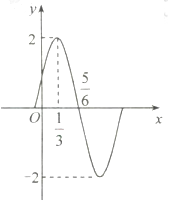 已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.
已知函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|ϕ|<\frac{π}{2}})$的图象(部分)如图所示.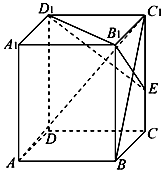 在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.
在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.