题目内容
已知定义在R上的函数f(x)满足条件f(x+
)=-f(x),且函数y=f(x-
)为奇函数,给出以下四个命题:
①函数f(x)的最小正周期是
;
②函数f(x)的图象关于点(-
,0)对称;
③函数f(x)为R上的偶函数;
④函数f(x)为R上的单调函数.
其中真命题的个数是( )
| 3 |
| 2 |
| 3 |
| 4 |
①函数f(x)的最小正周期是
| 3 |
| 2 |
②函数f(x)的图象关于点(-
| 3 |
| 4 |
③函数f(x)为R上的偶函数;
④函数f(x)为R上的单调函数.
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:函数的周期性,抽象函数及其应用
专题:函数的性质及应用
分析:由“f(x+
)=-f(x)”可得周期为3,由“且函数y=f(x-
)为奇函数”可得y=f(x)的对称性,然后两者结合以及利用代数变换或图象变换对四个选项做出判断.
| 3 |
| 2 |
| 3 |
| 4 |
解答:
解:∵对任意的x∈R,函数f(x)满足条件f(x+
)=-f(x),∴f(x+3)=f(x+
+
)=-f(x+
)=f(x),∴f(x)的最小正周期是3,故①④是假命题;
∵函数y=f(x-
)为奇函数,∴y=f(x-
)的图象关于原点对称,将y=f(x-
)的图象向左平移
个单位得y=f(x)的图象,∴函数f(x)的图象关于(-
,0)对称,故②是真命题;
∵y=f(x-
)为奇函数,∴f(-x-
)=-f(x-
),令t=x-
,代入上式得f(-t-
)=-f(t),即f(-x-
)=-f(x),结合f(x+
)=-f(x),∴f(-x-
)=-f(x+
),再令y=x+
,则由上式得f(-y)=f(y)恒成立,所以y=f(x)是偶函数,故③是真命题.所以,真命题共两个.
故选B
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∵函数y=f(x-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∵y=f(x-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故选B
点评:本题综合考查了抽象函数的奇偶性、周期性,因为没有具体的解析式,所以准确理解每个关系式的意义是解题关键,能结合图象理解的尽量结合图象,使问题直观化,具体化.

练习册系列答案
相关题目
若函数f(x)=
有且只有一个零点,则实数b等于( )
|
| A、-e | B、-1 | C、1 | D、e |
复数z=
的共轭复数是( )
| i |
| 1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
将角-
π写成α+2kπ(k∈Z,0≤α<2π)的形式,正确的是( )
| 27 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
在△ABC中,角A,B,C所对的边分别为5,7,8,则∠B的大小是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
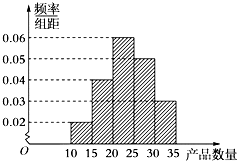 为了调查某厂2000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )
为了调查某厂2000名工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训,则这2位工人不在同一组的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
若点A(1,m-1,1)和点B(-1,-3,-1)关于原点对称,则m=( )
| A、-4 | B、4 | C、2 | D、-2 |
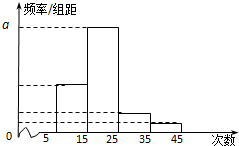 对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,
对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,