题目内容
17.若C${\;}_{2n}^{3}$=10C${\;}_{n}^{3}$,求n的值.分析 根据组合数公式,列出方程,解方程即可.
解答 解:∵C${\;}_{2n}^{3}$=10C${\;}_{n}^{3}$,
∴$\frac{2n•(2n-1)•(2n-2)}{3×2×1}$=10×$\frac{n(n-1)(n-2)}{3×2×1}$,
化简得2(2n-1)=5(n-2),
解得n=8.
点评 本题考查了组合数公式的应用问题,是基础题目.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
10.若(x-a)2($\frac{1}{x}$-1)4的展开式中常数项为15,则a的值为( )
| A. | 1 | B. | 8 | C. | -1或9 | D. | 1或-9 |
6.已知集合A={x|3x2-5x-2≥0},B={x|x≤$\frac{3}{2}$},则(∁RA)∩B=( )
| A. | [-$\frac{1}{3}$,$\frac{3}{2}$] | B. | (-$\frac{1}{3}$,$\frac{3}{2}$] | C. | (-2,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,2) |
9.两名男生和两名女生随机站成一排,则男生不相邻且女生也不相邻的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
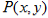 满足方程
满足方程 .
. 距离的最小值;
距离的最小值; ,若点
,若点 之间的最短距离为
之间的最短距离为 ,求满足条件的实数
,求满足条件的实数 的取值.
的取值.