题目内容
12.已知函数f(x)=log2(2x+$\sqrt{4{x}^{2}+3t}$)为奇函数,则实数t的值为$\frac{1}{3}$.分析 由f(x)为奇函数便有f(-x)=-f(x),即得到$lo{g}_{2}(-2x+\sqrt{4{x}^{2}+3t})$=$-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})$,分子有理化并进行对数的运算便可得到$lo{g}_{2}(3t)-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})$=$-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})$,这样便可得出3t=1,从而求出实数t的值.
解答 解:f(x)为奇函数;
∴f(-x)=-f(x);
即$lo{g}_{2}(-2x+\sqrt{4{x}^{2}+3t})=lo{g}_{2}\frac{3t}{2x+\sqrt{4{x}^{2}+3t}}$=$lo{g}_{2}3t-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})=-lo{g}_{2}(2x+\sqrt{4{x}^{2}+3t})$;
∴log2(3t)=0;
∴3t=1;
∴$t=\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查奇函数的定义,分子有理化和平方差公式,以及对数的运算.

练习册系列答案
相关题目
6.已知集合A={x|y=$\sqrt{x-4}$},B={x|-1≤2x-1≤0},则∁RA∩B=( )
| A. | (4,+∞) | B. | [0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,4] | D. | (1,4) |
7.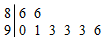 如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
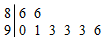 如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )| A. | 93,91 | B. | 86,93 | C. | 93,92 | D. | 86,91 |
4.2015年秋季开学之际,某校高一数学老师为了解学生的计算能力,先给出了一组计算测试题,全校学生完成时间在[20,40)(单位:分钟),各区间学生频率如下表:
若全校共有高一新生1000人.
(1)若学校规定完成时间不低于30分钟的要进行强化训练,试试估计全校参加强化训练的学生人数;
(2)若从全校按照完成时间,利用分层抽样的方法抽取10人.
①若从抽取的这10人中随机抽取1人,求他完成时间恰好在[30,40)的概率;
②若一节课为45分钟,从开始上课即进行测试,从这10人中随机抽取2人,求这两人所用测试时间都不超过30分钟的概率.
| 完成时间 | 频率 |
| [20,25) | 0.2 |
| [25,30) | 0.5 |
| [30,35) | 0.2 |
| [35,40) | 0.1 |
(1)若学校规定完成时间不低于30分钟的要进行强化训练,试试估计全校参加强化训练的学生人数;
(2)若从全校按照完成时间,利用分层抽样的方法抽取10人.
①若从抽取的这10人中随机抽取1人,求他完成时间恰好在[30,40)的概率;
②若一节课为45分钟,从开始上课即进行测试,从这10人中随机抽取2人,求这两人所用测试时间都不超过30分钟的概率.