题目内容
9.在△ABC中,a,b,c分别为角A,B,C所对的边,S为△ABC的面积,且S=$\frac{{\sqrt{3}}}{4}$(a2-b2-c2).(I)求角A的大小;
(II)若a=2$\sqrt{7}$,b>c,D为BC的中点,且AD=$\sqrt{3}$,求sinC的值.
分析 (I)由已知及三角形面积公式,同角三角函数基本关系式可求得$tanA=-\sqrt{3}$,结合范围A∈(0,π),即可得解A的值.
(II)由D为BC的中点,可得$BD=DC=\sqrt{7}$,$AD=\sqrt{3}$,利用cos∠ADB=-cos∠ADC结合余弦定理可得b2+c2=20,结合$\frac{{{b^2}+{c^2}-28}}{2bc}=cos\frac{2π}{3}=-\frac{1}{2}$,可求bc=8,进而可求b,c的值,利用正弦定理即可得解sinC的值.
解答 (本题满分为12分)
解:(I)由已知得$\frac{1}{2}bcsinA=\frac{{\sqrt{3}}}{4}({a^2}-{b^2}-{c^2})$,…(1分)
∴$sinA=-\sqrt{3}\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$.…(2分)
即$sinA=-\sqrt{3}cosA$.…(3分)
∴$tanA=-\sqrt{3}$.…(4分)
又∵A∈(0,π),$A=\frac{2π}{3}$,…(6分)
(II)由cos∠ADB=-cos∠ADC得:$\frac{{A{D^2}+B{D^2}-A{B^2}}}{2AD•BD}=-\frac{{A{D^2}+D{C^2}-A{C^2}}}{2AD•DC}$,
又∵D为BC的中点,
∴$BD=DC=\sqrt{7}$,$AD=\sqrt{3}$,
∴AB2+AC2=20,即b2+c2=20.…(8分)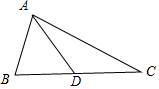
又∵$\frac{{{b^2}+{c^2}-28}}{2bc}=cos\frac{2π}{3}=-\frac{1}{2}$,
∴bc=8.…(9分)
又∵b>c,∴b=4,c=2,…(10分)
∴$sinC=\frac{csinA}{a}=\frac{{2•\frac{{\sqrt{3}}}{2}}}{{2\sqrt{7}}}=\frac{{\sqrt{21}}}{14}$.…(12分)
点评 本题主要考查了三角形面积公式,同角三角函数基本关系式,余弦定理,正弦定理在解三角形中的应用,考查了数形结合思想和转化思想,属于中档题.

| A. | cosβ=2cosα | B. | cos2β=2cos2α | C. | cos2β+2cos2α=0 | D. | cos2β=2cos2α |
| A. | 若α⊥β,l?α,n?β,则l⊥n | B. | 若l⊥α,l∥β,则α⊥β | ||
| C. | 若l⊥n,m⊥n,则l∥n | D. | 若α⊥β,l?α,则l⊥β |
| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | (1,+∞) | D. | (-∞,-1) |