Question

已知正四面体ABCD的棱长为1，M为AC的中点，P在线段DM上，则（AP+BP）²的最小值为

 

．

Answer 1

考点：多面体和旋转体表面上的最短距离问题

专题：综合题,空间位置关系与距离

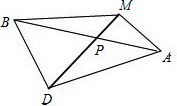
分析：把平面BMD及平面AMD以DM为折线展平，三角形DAM是正三角形的一半，故在平面BMAD中，连接BA，与MD相交于P点，则AP+BP为最短距离，再利用余弦定理即可得出．

解答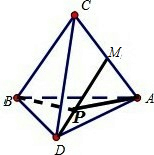： 解：由于各棱长均为1的四面体是正四面体
把平面BMD及平面AMD以DM为折线展平，三角形DAM是正三角形的一半
DM=

3

2

，AM=

1

2

，AD=1，BM=

3

2

，BD=1
故在平面BEAD中，连接BA，与MD相交于P点，则AP+BP为最短距离，
在三角形BMD中，根据余弦定理，
cos∠BMD=

3 4 + 3 4 -1

2• 3 2 • 3 2

=

1

3

，∴sin∠BMD=

2 2

3

，
cos∠DMB=cos（90°+∠BMC）=-sin∠BMC=-

2 2

3

，
∴BA²=BM²+AM²-2BM•AM•cos∠AMB=

3

4

+

1

4

-2•

3

2

•

1

2

•（-

2 2

3

）=1+

6

3

．
故答案为：1+

6

3

．

点评：本题考查棱锥的结构特征，其中把平面BMD及平面AMD以DM为折线展平，是解题的关键．