题目内容
9.已知函数$f(x)=\left\{{\begin{array}{l}{{2^{1-x}},x≤1}\\{1-log_2^x,x>1}\end{array}}\right.$,则满足f(x)≤4的x取值范围是( )| A. | [-1,+∞) | B. | $[\frac{1}{8},+∞)$ | C. | $[-1,\frac{1}{8}]$ | D. | $[\frac{1}{8},1]$ |
分析 利用分段函数列出不等式组转化求解即可.
解答 解:函数$f(x)=\left\{{\begin{array}{l}{{2^{1-x}},x≤1}\\{1-log_2^x,x>1}\end{array}}\right.$,则满足f(x)≤4,
可得:$\left\{\begin{array}{l}{x≤1}\\{{2}^{1-x}≤4}\end{array}\right.$或$\left\{\begin{array}{l}{x>1}\\{1-lo{g}_{2}x≤4}\end{array}\right.$,
解得x∈[-1,1]或x∈(1,+∞).
函数$f(x)=\left\{{\begin{array}{l}{{2^{1-x}},x≤1}\\{1-log_2^x,x>1}\end{array}}\right.$,则满足f(x)≤4的x取值范围是:[-1,+∞).
故选:A.
点评 本题考查分段函数的应用,指数与对数不等式的解法,考查计算能力.

练习册系列答案
相关题目
18.有5件不同的商品,其中2件次品,3件正品,从中取出2件,至少有1件次品的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
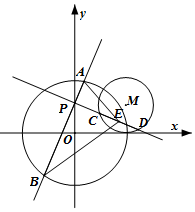 在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分别与
在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分别与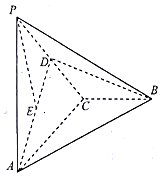 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.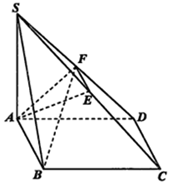 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2,$AB=\sqrt{6}$
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2,$AB=\sqrt{6}$