题目内容
18.执行如图所示的程序框图,如果输入的t=0.02,则输出的n=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,依次写出每次循环得到的s,m,n的值,可知当s=$\frac{1}{64}$时,不满足条件s>0.02,退出循环,输出n的值为6.
解答 解:模拟执行程序,可得
t=0.02,s=1,n=0,m=$\frac{1}{2}$,
执行循环体,s=$\frac{1}{2}$,m=$\frac{1}{4}$,n=1
满足条件s>0.02,执行循环体,s=$\frac{1}{4}$,m=$\frac{1}{8}$,n=2
满足条件s>0.02,执行循环体,s=$\frac{1}{8}$,m=$\frac{1}{16}$,n=3
满足条件s>0.02,执行循环体,s=$\frac{1}{16}$,m=$\frac{1}{32}$,n=4
满足条件s>0.02,执行循环体,s=$\frac{1}{32}$,m=$\frac{1}{64}$,n=5
满足条件s>0.02,执行循环体,s=$\frac{1}{64}$,m=$\frac{1}{128}$,n=6
不满足条件s>0.02,退出循环,输出n的值为6.
故选:A.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空题与选择题也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
3.2015年秋季开始,本市初一学生开始进行开放性科学实践活动,学生可以在全市范围内进行自主选课类型活动,选课数目、选课课程不限.为了了解学生的选课情况,某区有关部门随机抽取本区600名初一学生,统计了他们对于五类课程的选课情况,用“+”表示选,“-”表示不选.结果如表所示:
(1)估计学生既选了课程三,又选了课程四的概率;
(2)估计学生在五项课程中,选了三项课程的概率;
(3)如果这个区的某学生已经选了课程二,那么其余四项课程中他选择哪一项的可能性最大?
| 人数 课程 | 课程一 | 课程二 | 课程三 | 课程四 | 课程五 |
| 50 | + | + | - | + | - |
| 80 | + | + | - | - | - |
| 125 | + | - | + | - | + |
| 150 | - | + | + | + | - |
| 94 | + | - | - | + | + |
| 76 | - | - | + | + | - |
| 25 | - | - | + | - | + |
(2)估计学生在五项课程中,选了三项课程的概率;
(3)如果这个区的某学生已经选了课程二,那么其余四项课程中他选择哪一项的可能性最大?
10.已知某工程在很大程度上受当地年降水量的影响,施工期间的年降水量X(单位:mm)对工期延误天数Y的影响及相应的概率P如表所示:
在降水量X至少是100的条件下,工期延误不超过15天的概率为( )
| 降水量X | X<100 | 100≤X<200 | 200≤X<300 | X≥300 |
| 工期延误天数Y | 0 | 5 | 15 | 30 |
| 概率P | 0.4 | 0.2 | 0.1 | 0.3 |
| A. | 0.1 | B. | 0.3 | C. | 0.42 | D. | 0.5 |
6.某单位从包括甲、乙在内的5名应聘者中招聘2人,如果这5名应聘者被录用的机会均等,则甲、乙两人中至少有1人被录用的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
 与
与 轴交于
轴交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,与
,与 ,点
,点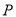 是
是 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点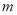 .
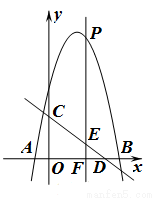
.
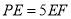 ,求
,求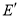 是点
是点 关于直线
关于直线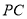 的对称点、是否存在点
的对称点、是否存在点 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点