题目内容
16.平面上有两定点A、B和动点P,|PA|=2|PB|,则动点P的轨迹为( )| A. | 椭圆 | B. | 圆 | C. | 双曲线 | D. | 抛物线 |
分析 设P点的坐标为(x,y),A(a,0),B(b,0),利用两点间的距离公式代入等式|PA|=2|PB|,化简整理得一个关于x,y的二元二次方程,所以点P的轨迹是一个圆.
解答 解:设A(a,0),B(b,0),设P点的坐标为(x,y),
动点P满足|PA|=2|PB|,
即|PA|2=4|PB|2,
则(x-a)2+y2=4[(x-b)2+y2],
即x2-2ax+a2+y2=4x2-8bx+4b2+4y2,
即3x2+3y2+2ax-4bx+4b2-a2=0
即x2+y2+$\frac{2}{3}$ax-$\frac{4}{3}$bx+$\frac{1}{3}$(4b2-a2)=0,
方程为x,y的二元二次方程,
则对应的轨迹是圆,
故选:B
点评 本题给出动点的轨迹,着重考查了两点间的距离公式、圆的一般方程,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
11.已知抛物线C:y2=6x的焦点为F,准线为l,点P在C上,点Q在l上,若$\overrightarrow{PF}$=$\overrightarrow{FQ}$,则直线PQ的斜率为( )
| A. | ±1 | B. | ±$\sqrt{2}$ | C. | ±$\sqrt{3}$ | D. | ±2 |
1.袋中有大小完全相同的2个红球和3个黑球,不放回地摸出两球,设“第一次摸出红球”为事件A,“摸得的两球同色”为事件B,则概率P(B|A)为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
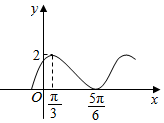 函数f(x)=Asin(ωx-φ)+1(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx-φ)+1(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.