题目内容
3.函数y=$\frac{cosx}{|sinx-2|-2}$是奇函数(填写奇偶性)分析 根据函数奇偶性的定义进行判断即可.
解答 解:∵-1≤sinx≤1,
∴y=$\frac{cosx}{|sinx-2|-2}$=$\frac{cosx}{2-sinx-2}$=-$\frac{cosx}{sinx}$,
则f(-x)=-$\frac{cos(-x)}{sin(-x)}$=$\frac{cosx}{sinx}$=-(-$\frac{cosx}{sinx}$)=-f(x),
则函数f(x)是奇函数,
故答案为:奇
点评 本题主要考查三角函数的奇偶性的判断,根据函数奇偶性的定义是解决本题的关键.比较基础.

练习册系列答案
相关题目
13.已知f(x)是定义在R上的增函数,函数y=f(x-1)的图象关于点(1,0)对称.若对任意的x,y∈R,不等式f(x2-6x-21)+f(2x)<0恒成立,x的取值范围是( )
| A. | (-3,7) | B. | (-9,2) | C. | ( 3,7) | D. | (2,9) |
11.已知i是虚数单位,则复数$\frac{(1-i)^{2}}{1+2i}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.如图是一个空间几何体的三视图,则该几何体的侧面积是( )
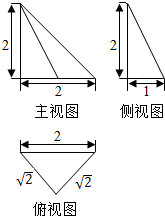

| A. | 3+$\sqrt{2}$+$\sqrt{3}$ | B. | $\frac{2}{3}$ | C. | 2+$\sqrt{2}$+$\sqrt{3}$ | D. | 5+$\sqrt{2}$ |
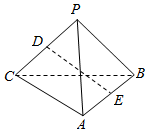 如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.