题目内容
已知抛物线x2=4y的焦点为F,过焦点F且不平行于x轴的动直线交抛物线于A、B两点,抛物线在A、B两点处的切线交于点M.

(1) 求证:A、M、B三点的横坐标成等差数列;
(2) 设直线MF交该抛物线于C、D两点,求四边形ACBD面积的最小值.
(1) 证明:由已知,得F(0,1),显然直线AB的斜率存在且不为0,
则可设直线AB的方程为y=kx+1(k≠0),A(x1,y1),B(x2,y2),
由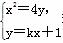 消去y,得x2-4kx-4=0,显然Δ=16k2+16>0.
消去y,得x2-4kx-4=0,显然Δ=16k2+16>0.
所以x1+x2=4k,x1x2=-4,
由x2=4y,得y=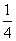 x2,所以y′=
x2,所以y′=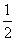 x, 所以,直线AM的斜率为kAM=
x, 所以,直线AM的斜率为kAM=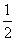 x1,
x1,
所以,直线AM的方程为y-y1=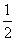 x1(x-x1),又x
x1(x-x1),又x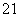 =4y1,
=4y1,
所以,直线AM的方程为x1x=2(y+y1) ①,
同理,直线BM的方程为x2x=2(y+y2) ②,
②-①并据x1≠x2得点M的横坐标x=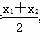 ,
,
即A、M、B三点的横坐标成等差数列.
(2) 解:由①②易得y=-1,所以点M的坐标为(2k,-1)(k≠0).
所以kMF=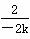 =-
=-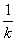 , 则直线MF的方程为y=-
, 则直线MF的方程为y=-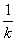 x+1,
x+1,
设C(x3,y3),D(x4,y4)
由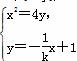 消去y,得x2+
消去y,得x2+ x-4=0,显然Δ=
x-4=0,显然Δ=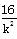 +16>0,
+16>0,
所以x3+x4=- ,x3x4=-4,
,x3x4=-4,
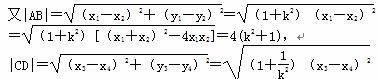
=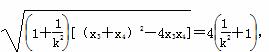
因为kMF·kAB=-1,所以AB⊥CD ,
所以SACBD=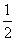 |AB|·|CD|=8
|AB|·|CD|=8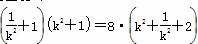 ≥32,
≥32,
当且仅当k=±1时,四边形ACBD面积取到最小值32.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 的值.
的值. +
+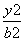 =1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
 =
=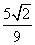 ,求实数m;
,求实数m;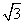 x,△AOB的面积为6
x,△AOB的面积为6 =1的离心率为________.
=1的离心率为________.