题目内容
3.已知在△ABC中,角A,B,C分别为△ABC的三个内角,若命题p:sinA>sinB,命题q:A>B,则p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 △ABC中,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,a>b?sinA>sinB.而a>b?A>B.即可判断出结论.
解答 解:△ABC中,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$=k>0,a>b?ksinA>ksinB?sinA>sinB.
而a>b?A>B.
∴△ABC中,sinA>sinB?A>B,即p?q.
∴p是q的充要条件.
故选:C.
点评 本题考查了正弦定理、三角形三边大小关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
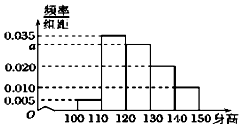 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).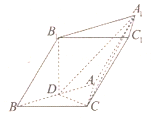 如图,在三棱柱ABC-A1B1C1中,D为AB的中点,CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.
如图,在三棱柱ABC-A1B1C1中,D为AB的中点,CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.