题目内容
14.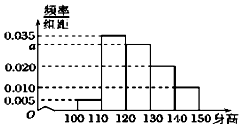 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).(1)求a的值;
(2)估计这所小学学生身高的众数、中位数、平均数.
分析 (1)根据频率直方图的矩形面积之和为1,即可求a.
(2)根据众数、中位数、平均数的定义,结合频率分布直方图进行估计即可.
解答 解:(1)由直方图得(0.005+0.035+a+0.02+0.01)×10=1,解得a=0.03
(2)数值最多的数在(110,120),则估计众数=115;
第一组的频率为0.005×10=0.05,
第二组的频率为0.035×10=0.35,
第三组的频率为0.03×10=0.3,
则前两组的频率之和为0.05+0.35=0.4,
则中位数位于第三组(120,130),靠前的部分,估计中位数=123.3;
第四组的频率为0.02×10=0.2,
第五组的频率为0.01×10=0.1,
则平均数=105×0.05+115×0.35+125×0.3+135×0.2+145×0.1=124.5
点评 本题主要考查频率分布直方图的应用,以及众数、中位数、平均数的求解,考查学生的运算能力.

练习册系列答案
相关题目
9.双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的渐近线方程为( )
| A. | y=±$\frac{3}{4}$x | B. | y=±$\frac{4}{3}$x | C. | y=±$\frac{3}{5}$x | D. | y=±$\frac{5}{3}$x |
9.利用独立性检验考察两个分类变量X与Y是否有关系时,若K2的观测值k=6.132,则有97.5%的把握认为“X与Y有关系”.
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
19.命题“若x≥1,则2x+1≥3”的逆否命题为( )
| A. | 若2x+1≥3,则x≥1 | B. | 若2x+1<3,则x<1 | C. | 若x≥1,则2x+1≥3 | D. | 若x<1,则2x+1≥3 |
6.双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的左右焦点分别为F1,F2,P是双曲线上的点,且∠F1PF2=90°,则△F1PF2的面积S=( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
3.已知在△ABC中,角A,B,C分别为△ABC的三个内角,若命题p:sinA>sinB,命题q:A>B,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |