题目内容
已知函数f（x）的定义域为[0，1]，求f（x2+1）的定义域．
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据复合函数定义域之间的关系即可得到结论．
解答：
解：∵函数f（x）的定义域为[0，1]，
∴0≤x2+1≤1，
∵x2+1≥1
则x2+1=1，
∴x=0
即函数f（x）的定义域为{0}，
∴0≤x2+1≤1，
∵x2+1≥1
则x2+1=1，
∴x=0
即函数f（x）的定义域为{0}，
点评：本题主要考查函数的定义域的求解，根据复合函数定义域之间的关系是解决本题的关键．
练习册系列答案
相关题目
已知向量
，
满足：|
|=1，|
|=2，|
-
|=2则|
+
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
如图，在空间四边形ABCD中，AB=BC=CD=DA=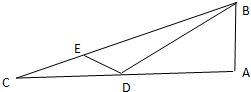
如图，在Rt△ABC中，∠A=90°，D是AC上一点，E是BC上一点，若AB=