题目内容
已知数列{an}满足a1=2,an+1=an+2n,n∈N+.
(1)求证:a2是a1,a3的等比中项;
(2)求数列{an}的通项公式.
(1)求证:a2是a1,a3的等比中项;
(2)求数列{an}的通项公式.
考点:数列递推式,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知结合数列递推式求出a2,a3的值,由此可得a2是a1,a3的等比中项;
(2)在数列递推式中分别取n=1,2,3,…,然后利用累加法求得数列通项公式.
(2)在数列递推式中分别取n=1,2,3,…,然后利用累加法求得数列通项公式.
解答:
(1)证明:由a1=2,an+1=an+2n,得a2=a1+2=2+2=4,a3=a2+2×2=4+4=8,
∵a22=42=2×8=a1a3,∴a2是a1,a3的等比中项;
(2)解:由a1=2,an+1=an+2n,得:
a2=a1+2×1,
a3=a2+2×2,
a4=a3+2×3,
…
an=an-1+2(n-1).
∴an=a1+2[1+2+3+…+(n-1)]=2+2×
=2+n2-n.
∵a22=42=2×8=a1a3,∴a2是a1,a3的等比中项;
(2)解:由a1=2,an+1=an+2n,得:
a2=a1+2×1,
a3=a2+2×2,
a4=a3+2×3,
…
an=an-1+2(n-1).
∴an=a1+2[1+2+3+…+(n-1)]=2+2×
| (1+n-1)(n-1) |
| 2 |
点评:本题考查了数列递推式,考查了累加法求数列的通项公式,是中档题.

练习册系列答案
相关题目
已知定义在R上的函数f(x)=
,且f(x+2)=f(x),则方程f(x)=
在区间[-5,1]上的所有实数之和为( )
|
| 2x+5 |
| x+2 |
| A、-5 | B、-6 | C、-7 | D、-8 |
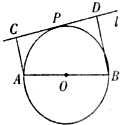 如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.