题目内容
19.已知集合$A=\left\{{x∈R\left|{\frac{x-6}{x+2}≤0}\right.}\right\}$,$B=\left\{{x∈R\left|{(x-m)(x+m-1)≤0,m>\frac{1}{2}}\right.}\right\}$,且“x∈A”是“x∈B”的充分不必要条件,求实数m的取值范围.分析 利用一元二次不等式的解法化简集合A,B,由“x∈A”是“x∈B”的充分不必要条件,可得A?B,即可得出.
解答 解:由$\frac{x-6}{x+2}$≤0,可得$\left\{\begin{array}{l}{(x+2)(x-6)≤0}\\{x+2≠0}\end{array}\right.$,解得-2<x≤6.
∴集合$A=\left\{{x∈R\left|{\frac{x-6}{x+2}≤0}\right.}\right\}$=(-2,6].
同理可得:$B=\left\{{x∈R\left|{(x-m)(x+m-1)≤0,m>\frac{1}{2}}\right.}\right\}$=[-m+1,m],
∵“x∈A”是“x∈B”的充分不必要条件,
∴A?B,
∴$\left\{\begin{array}{l}{-m+1<-2}\\{6≤m}\end{array}\right.$,解得m≥6.
∴实数m的取值范围是m≥6.
点评 本题考查了一元二次不等式的解法、不等式的性质、简易逻辑的判定方法、集合的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.若函数f(x)为定义域D上的单调函数,且存在区间[a,b]⊆D(其中a<b),使得当x∈[a,b]时,f(x)的取值范围恰为[a,b],则称函数f(x)是D上的正函数.若函数g(x)=x2-m是(-∞,0)上的正函数,则实数m的取值范围为( )
| A. | $(-1,-\frac{3}{4})$ | B. | $(-\frac{3}{4},0)$ | C. | $(\frac{3}{4},1)$ | D. | $(1,\frac{5}{4})$ |
7.威力实施“爱的教育”实践活动,宇华教育集团决定举行“爱在宇华”教师演讲比赛.焦作校区决定从高中部、初中部、小学部和幼教部这四个部门选出12人组成代表队代表焦作校区参赛,选手来源如下表:
焦作校区选手经过出色表现获得冠军,现要从中选出两名选手代表冠军队发言.
(1)求这两名队员来自同一部门的概率;
(2)设选出的两名选手中来自高中部的人数为ξ,求随机变量ξ的分布列及数学期望Eξ.
| 部门 | 高中部 | 初中部 | 小学部 | 幼教部 |
| 人数 | 4 | 4 | 2 | 2 |
(1)求这两名队员来自同一部门的概率;
(2)设选出的两名选手中来自高中部的人数为ξ,求随机变量ξ的分布列及数学期望Eξ.
14.以下给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2016}$的值的一个流程图(如图所示),其中判断框内应填入的条件是( )
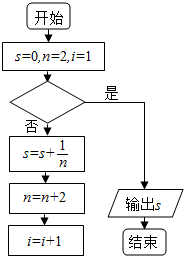

| A. | i>2016 | B. | i<2016 | C. | i>1008 | D. | i<1008 |
