题目内容

14．以下给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2016}$的值的一个流程图（如图所示），其中判断框内应填入的条件是（　　）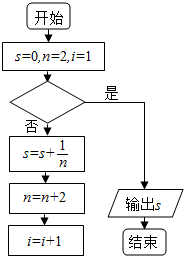
A．i＞2016B．i＜2016C．i＞1008D．i＜1008

分析 写出前三次循环得到的结果，找出规律，得到要输出的S在第1008次循环中结果中，此时的i满足判断框中的条件，得到判断框中的条件

解答 解：经过第一次循环得到 S=$\frac{1}{2}$，i=2，此时的i不满足判断框中的条件
经过第二次循环得到 S=$\frac{1}{2}$+$\frac{1}{4}$，i=3，此时的i不满足判断框中的条件
经过第三次循环得到 S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$，i=4，此时的i不满足判断框中的条件
…
经过第1008次循环得到 S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2016}$，i=1009，此时的i不满足判断框中的条件
接下来，当i=1009时，满足判断框中的条件，执行输出
故判断框中的条件是i＞1008（或者i≥1009）
故选：C

点评 本题主要考查了循环结构，解决程序框图中的循环结构时，常采用写出前几次循环的结果，从中找出规律，属于基础题．

练习册系列答案
相关题目
4．如图，正四棱锥P-ABCD的底面长为2，侧棱长为$\sqrt{10}$，点O为底面ABCD的中心
（Ⅰ）求证：PA⊥BD；
（Ⅱ）求二面角C-PB-D的余弦值．
5．已知函数f（log2x）=x-$\frac{1}{x}$
（1）求函数f（x）的表达式，并说明函数的单调性、奇偶性（无需证明）；
（2）设集合A=$\{x|x=sinθ+cosθ，θ∈（-\frac{π}{2}，0）\}$，若函数y=f（x）（x∈A），且f（1-m）+f（1-m2）＜0，求实数 m的取值范围；
（3）若不等式2tf（2t）+mf（t）≥0对于t∈[1，2]恒成立，求实数 m的取值范围．
2．已知曲线y=x+lnx在点（1，1）处的切线与曲线y=ax2+（a+2）x+l相切．求不等式x2-（a+l）x+a≤0的解集．
9．6本相同的数学书和3本不相同的语文书分给9个人，每人1本，共有不同分法（　　）
A．C${\;}_{9}^{3}$B．A${\;}_{9}^{3}$C．A${\;}_{9}^{6}$D．A${\;}_{9}^{3}$•A${\;}_{3}^{3}$
19．已知集合$A=\left\{{x∈R\left|{\frac{x-6}{x+2}≤0}\right.}\right\}$，$B=\left\{{x∈R\left|{（x-m）（x+m-1）≤0，m＞\frac{1}{2}}\right.}\right\}$，且“x∈A”是“x∈B”的充分不必要条件，求实数m的取值范围．
6．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点M（$\sqrt{2}$，1），且焦点为F1（-$\sqrt{2}$，0）
（Ⅰ）求椭圆C的方程；
（Ⅱ）当过点P（4，0）的动直线l与椭圆C相交于两不同点A，B时，在线段AB上取点Q，满足$\frac{|\overrightarrow{AP}|}{|\overrightarrow{PB}|}$=$\frac{|\overrightarrow{AQ}|}{|\overrightarrow{QB}|}$，证明：点Q总在某定直线上．
3．方程x2+y2+2x+4y+6=0表示的图形是（　　）
A．点B．两条直线C．圆D．没有图形
4．已知函数$f（x）=lnx-\frac{1}{2}a{x^2}+（a-1）x（a∈$R）．
（Ⅰ）当a＞-1时，求f（x）的单调区间；
（Ⅱ）对于曲线上的不同两点A（x1，y1）、B（x2，y2），如果存在曲线上的点M（x0，y0），且x1＜x0＜x2，使得曲线在点M处的切线l∥AB，则称直线AB存在“伴随切线”．特别地，当${x_0}=\frac{{{x_1}+{x_2}}}{2}$时，又称直线AB存在“中值伴随切线”．
试问：在函数y=f（x）的图象上是否存在两点A、B，使得直线AB存在“中值伴随切线”？若存在，求出A、B的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网