题目内容
15．计算0.5-2×（$\frac{27}{8}$）${\;}^{\frac{1}{3}}$+（$\root{4}{9}$）2．分析 直接利用有理指数幂的运算法则化简求解即可．
解答 解：0.5-2×（$\frac{27}{8}$）${\;}^{\frac{1}{3}}$+（$\root{4}{9}$）2
=4×$\frac{3}{2}$+3
=9．
点评 本题考查有理指数幂的运算法则的应用，考查计算能力．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
3．已知A={x|y=$\frac{1}{x-2}$+1nx}，B={y|y=$\sqrt{16-{2}^{x}}$}，则A∩B=（ ）
| A． | （0，4] | B． | [0，2）U（2，4） | C． | （0，2）U（2，4） | D． | [0，2）U（2，4] |
10．已知函数y=sin（ωx+φ）（ω＞0，0＜φ＜π）满足f（-x）=f（x），其图象与直线y=1的某两个交点横坐标分别为x1，x2，且|x1-x2|的最小值为π，则（ ）
| A． | $ω=\frac{1}{2}$，φ=$\frac{π}{4}$ | B． | ω=2，φ=$\frac{π}{4}$ | C． | $ω=\frac{1}{2}$，φ=$\frac{π}{2}$ | D． | ω=2，φ=$\frac{π}{2}$ |
1．
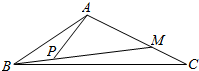如图，已知△ABC中，点M在线段AC上，点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2，若$|\overrightarrow{AB}|$=2，$|\overrightarrow{AC}|$=3，∠BAC=120°，则$\overrightarrow{AP}•\overrightarrow{BC}$的值为（ ）
如图，已知△ABC中，点M在线段AC上，点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2，若$|\overrightarrow{AB}|$=2，$|\overrightarrow{AC}|$=3，∠BAC=120°，则$\overrightarrow{AP}•\overrightarrow{BC}$的值为（ ）| A． | -2 | B． | 2 | C． | $\frac{2}{3}$ | D． | $-\frac{11}{3}$ |
5．函数y=|x-1|与y=lgx图象交点个数为（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
6．函数$f（x）=\frac{2x-3}{3x+1}，x∈（-1，-\frac{1}{3}）∪（-\frac{1}{3}，1）$的值域是（ ）
| A． | $（-∞，-\frac{1}{4}）∪（\frac{5}{2}，+∞）$ | B． | $（-\frac{1}{4}，\frac{5}{2}）$ | C． | $（-\frac{1}{4}，0）∪（\frac{5}{2}，+∞）$ | D． | $（-∞，-\frac{1}{4}）∪（0，\frac{5}{2}）$ |