题目内容
已知数列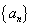 的前
的前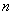 项和为
项和为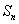
(1)若数列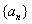 是等比数列,满足
是等比数列,满足 ,
, 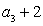 是
是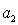 ,
,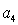 的等差
的等差 中项,求数列
中项,求数列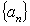 的通项公式;
的通项公式;
(2)是否存在等差数列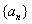 ,使对任意
,使对任意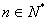 都有
都有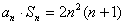 ?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.
?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.
(1)设等比数列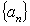 的首项为
的首项为 ,公比为
,公比为 ,
,
依题意,有 即
即
由  得
得  ,解得
,解得 或
或 .
.
当 时,不合题意舍;
时,不合题意舍;
当 时,代入(2)得
时,代入(2)得 ,所以,
,所以, .
.
(2)假设存在满足条件的数列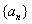 ,设此数列的公差为
,设此数列的公差为 ,则
,则
方法1: ,得
,得
 对
对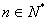 恒成立,
恒成立,
则
解得 或
或 此时
此时 ,或
,或 .
.
故存在 等差数列
等差数列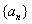 ,使对任意
,使对任意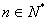 都有
都有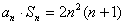 .其中
.其中 ,
,
或 .
.
方法2:令 ,
, ,得
,得 ,
,
令 ,得
,得 ,
, 

①当 时,得
时,得 或
或 ,
,
若 ,则
,则 ,
, ,
, ,对任意
,对任意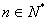 都有
都有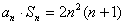 ;
;
若 ,则
,则 ,
, ,
, ,不满足
,不满足 .
.
②当 时,得
时,得 或
或 ,
,
若 ,则
,则 ,
, ,
, ,对任意
,对任意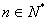 都有
都有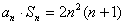 ;
;
若 ,则
,则 ,
, ,
, ,不满足
,不满足 .
.
综上所述,存在等差数列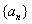 ,使对任意
,使对任意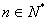 都有
都有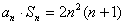 .其中
.其中 ,或
,或 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
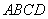 是正方形,
是正方形, ⊥面
⊥面 问图中有 对互相垂直的平面.
问图中有 对互相垂直的平面.
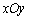 中,
中,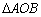 和
和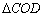 为两等腰直角三角形,
为两等腰直角三角形,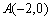 ,C(a,0)(a>0).设
,C(a,0)(a>0).设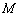 ,
,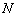 .
.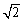 ,若存在,求此时⊙N的标准方程;若不存在,说明理由.
,若存在,求此时⊙N的标准方程;若不存在,说明理由.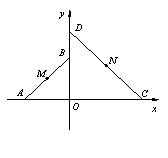
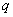 ,其前
,其前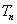 ,并且满足条件
,并且满足条件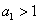 ,
, ,
,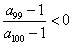 .给出下列结论:①
.给出下列结论:① ;②
;②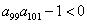 ;③
;③ 的值是
的值是 成立的最大自然数
成立的最大自然数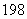 ,其中正确的结论是__________.
,其中正确的结论是__________. 前
前
 ,关于数列
,关于数列 则
则 ,则
,则 成等比数列;
成等比数列; 则
则 的定义域为 .
的定义域为 .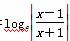 (0<a<1)的说法正确的为________.(填序号)
(0<a<1)的说法正确的为________.(填序号)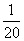 (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.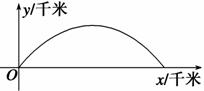
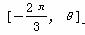 上的最大值为1,
上的最大值为1, 则θ的值是________.
则θ的值是________.