题目内容
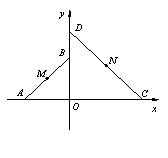
如图,平面直角坐标系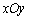 中,
中,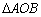 和
和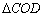 为两等腰直角三角形,
为两等腰直角三角形,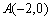 ,C(a,0)(a>0).设
,C(a,0)(a>0).设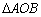 和
和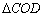 的外接圆圆心分别为
的外接圆圆心分别为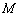 ,
,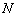 .
.
(1)若⊙M与直线CD相切,求直线CD的方程;
(2)若直线AB截⊙N所得弦长为4,求⊙N的标准方程;
(3)是否存在这样的⊙N,使得⊙N上有且只有三个点到直线AB的距离为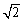 ,若存在,求此时⊙N的标准方程;若不存在,说明理由.
,若存在,求此时⊙N的标准方程;若不存在,说明理由.
(1)圆心 .∴圆
.∴圆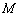 方程为
方程为 ,
,
直线CD方程为 .
.
∵⊙M与直线CD相切,∴圆心M到直线CD的距离d= ,
,
化简得:  (舍去负值).∴直线CD的方程为
(舍去负值).∴直线CD的方程为 .
.
(2)直线AB方程为: ,圆心N
,圆心N .
.
∴圆心N到直线AB距离为 .
.
∵直线AB截⊙N的所得弦长为4,∴ .
.
∴a=± (舍去负值) . ∴⊙N的标准方程为
(舍去负值) . ∴⊙N的标准方程为
 .
.
(3)存在.
由(2)知,圆心N到直线AB距离为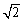 (定值),且AB⊥CD始终成立,
(定值),且AB⊥CD始终成立,
∴当且仅当圆N半径 ,即a=4时
,即a=4时 ,⊙N上有且只有三个点到直线AB的距离为
,⊙N上有且只有三个点到直线AB的距离为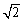 .
.
此时, ⊙N的标准方程为 .
.

练习册系列答案
相关题目
 的实部为
的实部为 ,虚部为
,虚部为 ,则
,则 =____
=____ ____.
____. 中,
中, ,那么当该棱锥的体积取最大时,高为 .
,那么当该棱锥的体积取最大时,高为 .  与直线y=k(x-2)+4有两个不同交点,则实数k的取值范围是____.
与直线y=k(x-2)+4有两个不同交点,则实数k的取值范围是____. 为双曲线
为双曲线 的左准线与x轴的交点,点
的左准线与x轴的交点,点 ,若满足
,若满足 的点
的点 在双曲线上,则该双曲线的离心率为 .
在双曲线上,则该双曲线的离心率为 .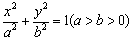 的离心率为
的离心率为 , 过点
, 过点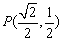 , 记椭圆的左顶点为
, 记椭圆的左顶点为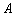 .
. 轴的直线
轴的直线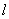 交椭圆于
交椭圆于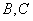 两点, 试求
两点, 试求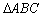 面积的最大值;
面积的最大值;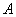 作两条斜率分别为
作两条斜率分别为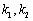 的直线交椭圆于
的直线交椭圆于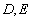 两点,且
两点,且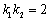 , 求证: 直线
, 求证: 直线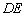 恒过一个定点.
恒过一个定点.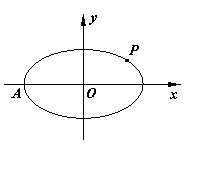
 的前
的前 项和
项和 是
是 ,若
,若 都是等差数列,且公差相等,则
都是等差数列,且公差相等,则 .
.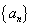 的前
的前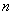 项和为
项和为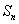
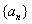 是等比数列,满足
是等比数列,满足 ,
, 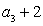 是
是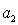 ,
,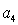 的等差
的等差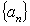 的通项公式;
的通项公式;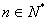 都有
都有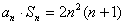 ?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.
?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由. 的减区间是____ ____,增区间是________.
的减区间是____ ____,增区间是________.