题目内容
10．某几何体的三视图如图所示，则它的表面积为（ ）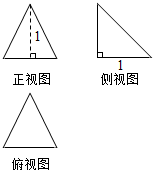
| A． | $\frac{{\sqrt{3}+\sqrt{7}+4}}{4}$ | B． | $\frac{{\sqrt{6}+2}}{2}$ | C． | $\frac{{\sqrt{2}+\sqrt{7}+1}}{2}$ | D． | $\frac{{\sqrt{2}+\sqrt{5}+1}}{2}$ |
分析 根据三视图判断几何体的形状，根据它的几何性质得出，利用三角形求出表面积．
解答 解：根据三视图得出该几何体为三棱锥，如图所示：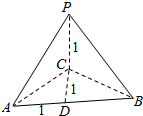
PC⊥面ABC，CD⊥AD于D，AB=1，CD=1，PC=1，
∴S△ABC=$\frac{1}{2}$×1×1=$\frac{1}{2}$，S△PAC=S△PBC=$\frac{1}{2}$×1×$\sqrt{{1}^{2}{+（\frac{1}{2}）}^{2}}$=$\frac{\sqrt{5}}{4}$，
S△PAB=$\frac{1}{2}$×1×$\sqrt{{1}^{2}{+1}^{2}}$=$\frac{\sqrt{2}}{2}$；
所以该三棱锥的表面积为S=$\frac{1}{2}$+2×$\frac{\sqrt{5}}{4}$+$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{5}+\sqrt{2}+1}{2}$．
故选：D．
点评 本题考查了空间几何体三视图的应用问题，解题的关键是根据三视图得出几何体的结构特征，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
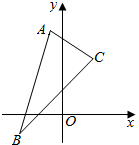已知△ABC三个顶点是A（-1，4），B（-2，-1），C（2，3）．