题目内容
10.已知A点坐标为(-1,0),B点坐标为(1,0),且动点M到A点的距离是4,线段MB的垂直平分线l交线段MA于点P.(1)求动点P的轨迹C方程;(2)若P是曲线C上的点,求k=|PA|•|PB|的最大值和最小值.
分析 (1)根据题意画出图形,利用垂直平分线转换线段的关系得到|PA|+|PB|=|PA|+|PM|=|AM|=4,据椭圆的定义即可得到动点P的轨迹方程.
(2)利用配方法,即可得出结论.
解答 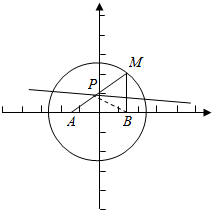 解:(1)由线段MB的垂直平分线l交MA于点P知,PB=PM
解:(1)由线段MB的垂直平分线l交MA于点P知,PB=PM
故|PA|+|PB|=|PA|+|PM|=|AM|=4,
即P点的轨迹为以A、B为焦点的椭圆,中心为(0,0),
故P点的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)∵|PA|+|PB|=4,
∴k=|PA|•|PB|=|PA|•(4-|PA|)=-(|PA|-2)2+4,
∵1≤|PA|≤3,
∴|PA|=2,k=|PA|•|PB|取最大值4;|PA|=1或,k=|PA|•|PB|取最小值3.
点评 定义法:运用解析几何中一些常用定义(例如圆锥曲线的定义),可从曲线定义出发直接写出轨迹方程,或从曲线定义出发建立关系式,从而求出轨迹方程.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
1.设$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(-3,4),则2$\overrightarrow{a}$+$\overrightarrow{b}$等于( )
| A. | (3,4) | B. | (1,2) | C. | -7 | D. | 3 |
18.已知函数f(x)=cosωx(sinωx+$\sqrt{3}$cosωx)(ω>0),如果存在实数x0,使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
| A. | $\frac{1}{2016π}$ | B. | $\frac{1}{4032π}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{4032}$ |
4. 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
 已知函数f(x)=|x-1|+|x-2|.
已知函数f(x)=|x-1|+|x-2|.