题目内容
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:规格类型 钢板规格 | A规格 | B规格 | C规格 |
第一种钢板 | 2 | 1 | 1 |
第二种钢板 | 1 | 2 | 3 |
今需A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需三种规格的成品,且使所用的钢板的张数最少？
思路分析：此为整点最优解问题,准确地作出可行域,是解答这类问题的关键.
解:设需截第一种钢板x张,第二种钢板y张,可得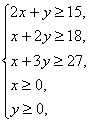
且x、y都是整数,求使z=x+y取得最小值时的x、y.
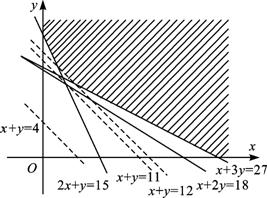
首先作出可行域,其次平移直线z=x+y,可知直线经过点(
),此时 x=
,y=
.z=x+y有最小值11
,但(
,
)不是最优解.
首先在可行域内打网格,其次推出点A(
,
)附近所有整点,接着平移直线l:x+y=0,会发现当平移至B(4,8)、C(3,9)时直线与原点的距离最近,即z的最小值为12.
练习册系列答案
优质课堂快乐成长系列答案
相关题目
要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格小钢板的块数如下表所示：
每张钢板的面积，第一种为1m2，第二种为2m2，今需要A、B、C三种规格的成品各12、15、27块，问各截这两种钢板多少张，可得所需三种规格成品，且使所用钢板面积最小？
| 类 型 | A规格 | B规格 | C规格 |
| 第一种钢板 | 1 | 2 | 1 |
| 第二种钢板 | 1 | 1 | 3 |
要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格的小钢板块数如下表：
|
要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格小钢板的块数如下表所示：
|
类 型 |
A规格 |
B规格 |
C规格 |
|
第一种钢板 |
1 |
2 |
1 |
|
第二种钢板 |
1 |
1 |
3 |
每张钢板的面积,第一种为
,第二种为
,今需要A、B、C三种规格的成品各12、15、27块,问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小？