题目内容
已知函数f(x)=
,x∈[0,1].
(1)求函数f(x)的值域;
(2)若f(x)与g(x)=x2-2ax,x∈[0,1]的最小值相同,求实数a的值.
| x2-2x-4 |
| x+2 |
(1)求函数f(x)的值域;
(2)若f(x)与g(x)=x2-2ax,x∈[0,1]的最小值相同,求实数a的值.
考点:函数的值域
专题:计算题,函数的性质及应用
分析:(1)由题意化简函数的表达式,并判断函数的单调性,从而求值域;
(2)由g(x)=x2-2ax,x∈[0,1]的最小值也为-2初步判断a的取值范围,从而简化讨论,求出实数a的值.
(2)由g(x)=x2-2ax,x∈[0,1]的最小值也为-2初步判断a的取值范围,从而简化讨论,求出实数a的值.
解答:
解:(1)f(x)=
=(x+2)+
-6,
其在[0,1]上是增函数,
故-2≤
≤-
,
故函数f(x)的值域为[-2,-
].
(2)∵函数f(x)=
,x∈[0,1]的最小值为-2,
∴g(x)=x2-2ax,x∈[0,1]的最小值也为-2;
又∵g(x)=(x-a)2-a2,∴-a2≤-2,且a>0;
即a≥
.
故g(x)=x2-2ax在[0,1]上是减函数,
则g(1)=1-2a=-2,解得,
a=
.
| x2-2x-4 |
| x+2 |
| 4 |
| x+2 |
其在[0,1]上是增函数,
故-2≤
| x2-2x-4 |
| x+2 |
| 5 |
| 3 |
故函数f(x)的值域为[-2,-
| 5 |
| 3 |
(2)∵函数f(x)=
| x2-2x-4 |
| x+2 |
∴g(x)=x2-2ax,x∈[0,1]的最小值也为-2;
又∵g(x)=(x-a)2-a2,∴-a2≤-2,且a>0;
即a≥
| 2 |
故g(x)=x2-2ax在[0,1]上是减函数,
则g(1)=1-2a=-2,解得,
a=
| 3 |
| 2 |
点评:本题考查了函数的值域的求法,用到了分离常数的方法,及函数的单调性,同时考查了分类讨论的思想,属于中档题.

练习册系列答案
相关题目
若x1,x2是方程2x2-4x+1=0的两个根,则
+
的值为( )
| x1 |
| x2 |
| x2 |
| x1 |
| A、6 | ||
| B、4 | ||
| C、3 | ||
D、
|
从装有2个白球和2个蓝球的口袋中任取2个球,那么对立的两个事件是( )
| A、“恰有一个白球”与“恰有两个白球” |
| B、“至少有一个白球”与“至少有-个蓝球” |
| C、“至少有-个白球”与“都是蓝球” |
| D、“至少有一个白球”与“都是白球” |
己知等差数列{an}的公差d=-1,若a2+a8=2,则该数列的前n项和Sn的最大值为( )
| A、5 | B、10 | C、15 | D、16 |
已知全集全集U={0,1,2,3,4},集合A={1,2,3},B={0,3,4},则A∩∁UB=( )
| A、{0,4} |
| B、{3,4} |
| C、{1,2} |
| D、x2-3x-10>0 |
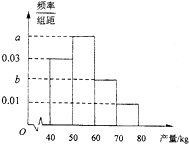 果农随机选取某类果树50株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,50],(50,60],(60,70],(70,80]进行分组,得到频率分布直方图如图,已知样本中产量在区间(50,60]上的果树株数是产量在区间(60,80]上的果树株数的
果农随机选取某类果树50株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,50],(50,60],(60,70],(70,80]进行分组,得到频率分布直方图如图,已知样本中产量在区间(50,60]上的果树株数是产量在区间(60,80]上的果树株数的