题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{1-\frac{x}{2},x<1}\end{array}$,若F(x)=f[f(x)+1]+m有两个零点x1,x2,则x1•x2的取值范围是( )| A. | [4-2ln2,+∞) | B. | ($\sqrt{e}$,+∞) | C. | (-∞,4-2ln2] | D. | (-∞,$\sqrt{e}$) |
分析 由题意可知:当x≥1时,f(x)+1≥1,f[f(x)+1]=ln(f(x)+1),当x<1,f(x)=1-$\frac{x}{2}$>$\frac{1}{2}$,f[f(x)+1]=ln(f(x)+1),f[f(x)+1]=ln(f(x)+1)+m=0,则x1x2=et(2-2t),t>$\frac{1}{2}$,设g(t)=et(2-2t),t>$\frac{1}{2}$,求导,利用导数求得函数的单调性区间,即可求得x1x2的取值范围.
解答 解:当x≥1时,f(x)=lnx≥0,
∴f(x)+1≥1,
∴f[f(x)+1]=ln(f(x)+1),
当x<1,f(x)=1-$\frac{x}{2}$>$\frac{1}{2}$,f(x)+1>$\frac{3}{2}$,
f[f(x)+1]=ln(f(x)+1),
综上可知:F[f(x)+1]=ln(f(x)+1)+m=0,
则f(x)+1=e-m,f(x)=e-m-1,有两个根x1,x2,(不妨设x1<x2),
当x≥1是,lnx2=e-m-1,当x<1时,1-$\frac{{x}_{1}}{2}$=e-m-1,
令t=e-m-1>$\frac{1}{2}$,则lnx2=t,x2=et,1-$\frac{{x}_{1}}{2}$=t,x1=2-2t,
∴x1x2=et(2-2t),t>$\frac{1}{2}$,
设g(t)=et(2-2t),t>$\frac{1}{2}$,
求导g′(t)=-2tet,
t∈($\frac{1}{2}$,+∞),g′(t)<0,函数g(t)单调递减,
∴g(t)<g($\frac{1}{2}$)=$\sqrt{e}$,
∴g(x)的值域为(-∞,$\sqrt{e}$),
∴x1x2取值范围为(-∞,$\sqrt{e}$),
故选:D.
点评 本题考查函数零点的判定,利用导数求函数的单调性及最值,考查计算能力,属于中档题.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| A. | p是假命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | B. | p是假命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | ||
| C. | P是真命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | D. | p是真命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 |
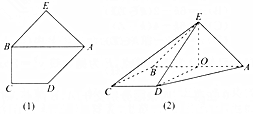 如图(1),在五边形BCDAE中,CD∥AB,∠BCD=90°,CD=BC=1,AB=2,△ABE是以AB为斜边的等腰直角三角形,现将△ABE沿AB折起,使平面ABE⊥平面ABCD,如图(2),记线段AB的中点为O.
如图(1),在五边形BCDAE中,CD∥AB,∠BCD=90°,CD=BC=1,AB=2,△ABE是以AB为斜边的等腰直角三角形,现将△ABE沿AB折起,使平面ABE⊥平面ABCD,如图(2),记线段AB的中点为O.