题目内容
在直角坐标平面上,有5个非零向量
、
、
、
、
,且
⊥
(k=1,2,3,4),各向量的横坐标和纵坐标均为非负实数,若|
|+|
|+|
|+|
|+|
|=l(常数),则|
+
+
+
+
|的最小值为 .
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| ak |
| ak+1 |
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
考点:两向量的和或差的模的最值
专题:平面向量及应用
分析:不妨设图形为:设
+
+
=(m,0),(m>0),
+
=(n,0),(n>0).
|
|+|
|+|
|=m,|
|+|
|=n.|
|+|
|+|
|+|
|+|
|=l(常数),
m+n=l.再利用基本不等式即可得出.
| a1 |
| a3 |
| a5 |
| a2 |
| a4 |
|
| a1 |
| a3 |
| a5 |
| a2 |
| a4 |
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
m+n=l.再利用基本不等式即可得出.
解答:
解:由5个非零向量
、
、
、
、
,且
⊥
(k=1,2,3,4),各向量的横坐标和纵坐标均为非负实数,(k=1,2,3,4),各向量的横坐标和纵坐标均为非负实数,不妨设图形为: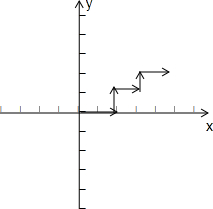
设
+
+
=(m,0),(m>0),
+
=(n,0),(n>0).
∴|
|+|
|+|
|=m,|
|+|
|=n.
∵|
|+|
|+|
|+|
|+|
|=l(常数),
∴m+n=l.
∴|
+
+
+
+
|=
≥
=
l.
当且仅当m=n=
l取等号.
∴|
+
+
+
+
|的最小值为
l.
故答案为:
l.
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| ak |
| ak+1 |

设
| a1 |
| a3 |
| a5 |
| a2 |
| a4 |
∴|
| a1 |
| a3 |
| a5 |
| a2 |
| a4 |
∵|
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
∴m+n=l.
∴|
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| m2+n2 |
| m+n | ||
|
| ||
| 2 |
当且仅当m=n=
| 1 |
| 2 |
∴|
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了向量的坐标运算、数量积运算及其性质、基本不等式,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
偶函数y=f(x),当x∈[0,∞)时,f(x)=x-1,则f(x-1)<0的解集为( )
| A、{x|-1<x<1} |
| B、{x|1<x<2 } |
| C、{x|0<x<2} |
| D、{x|-2<x<0或0<x<2} |
某几何体的三视图所图所示,则它的表面积为( )


A、20+
| ||
| B、24-π | ||
C、24+(
| ||
| D、20 |
函数y=f(x)在x=x0处可导,则
=( )
| lim |
| h→0 |
| f(x0-h)-f(x0+h) |
| h |
A、
| ||
B、-
| ||
| C、2f′(x0) | ||
| D、-2f′(x0) |
