题目内容
19.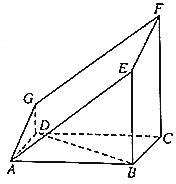 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.(Ⅰ)求证:BD⊥平面ADG;
(Ⅱ)求此多面体的全面积.
分析 (Ⅰ)在△BAD中,由余弦定理求得BD=$\sqrt{3}$,可得AB2=AD2+BD2,得AD⊥BD.再由已知可得CD⊥BD,由线面垂直的判定可得BD⊥平面ADG;
(Ⅱ)由已知可得,AG∥EF,AE∥GF,得四边形AEFG为平行四边形,然后求出各面面积得答案.
解答 (Ⅰ)证明:在△BAD中,∵AB=2AD=2,∠BAD=60°,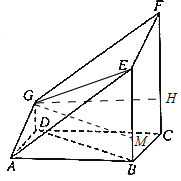
∴由余弦定理可得BD=$\sqrt{3}$,
则AB2=AD2+BD2,∴AD⊥BD.
在直平行六面体中,GD⊥平面ABCD,BD?平面ABCD,
∴GD⊥BD,
又AD∩GD=D,∴BD⊥平面ADG;
(Ⅱ)由已知可得,AG∥EF,AE∥GF,
∴四边形AEFG为平行四边形,
GD=AD=1,∴EF=AG=$\sqrt{2}$.
EB=AB=2,∴GF=AE=2$\sqrt{2}$.
过G作GH∥DC交CF于H,得FH=2,∴FC=3.
过G作GM∥DB交BE于M,得GM=DB=$\sqrt{3}$,ME=1,∴GE=2.
cos∠GAE=$\frac{8+2-4}{2×2\sqrt{2}×\sqrt{2}}=\frac{3}{4}$,∴sin∠GAE=$\frac{\sqrt{7}}{4}$.
${S}_{AEFG}=2×\frac{1}{2}×\sqrt{2}×2\sqrt{2}×\frac{\sqrt{7}}{4}=\sqrt{7}$.
该几何体的全面积S=$\sqrt{7}+2×\frac{1}{2}×1×\sqrt{3}+\frac{1}{3}×1×1+\frac{1}{2}×2×2$$+\frac{1}{2}×(1+3)×2+\frac{1}{2}×(2+3)×1=\sqrt{7}+\sqrt{3}+9$.
点评 本题考查直线与平面垂直的判定,考查柱、锥、台体表面积的求法,考查空间想象能力和思维能力,属中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
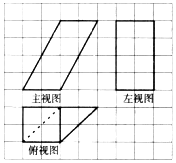
| A. | 16+4$\sqrt{5}$ | B. | 20+4$\sqrt{5}$ | C. | 16+8$\sqrt{5}$ | D. | 8+12$\sqrt{5}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (-1,1) | B. | [1,+∞) | C. | (1,+∞) | D. | (2,+∞) |
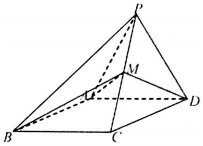 如图所示,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面ABCD是∠ABC=60°的菱形,M为PC的中点,PC=$\sqrt{6}$.
如图所示,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面ABCD是∠ABC=60°的菱形,M为PC的中点,PC=$\sqrt{6}$.